À partir de la définition (31) du vecteur accélération et de l'expression (19) du vecteur vitesse on a :

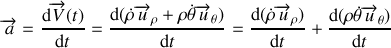
En utilisant les règles habituelles de dérivations d'un produit et les expressions (18) on a :

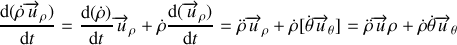
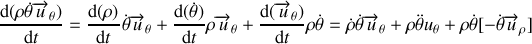
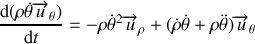
En regroupant et ordonnant les différents résultats on obtient l'expression :

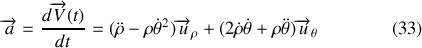
Le premier terme 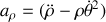correspond à la composante radiale de l'accélération et le second terme 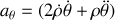est sa composante orthoradiale.