Nous nous plaçons ici purement dans le cadre de la mécanique. Pour cette raison, nous appréhendons l'énergie potentielle de façon simple et moins ambitieuse que ce que nous pourrions faire dans le cadre plus général de la thermodynamique.
Par définition le travail des forces conservatives ne dépend pas du chemin suivi mais uniquement de l'état initial et final. Le travail de ces forces peut donc s'exprimer à partir d'une fonction d'état appelée énergie potentielle
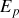. Pour des raisons qui apparaissent clairement au dans "énergie mécanique", nous conviendrons de la définition suivante :
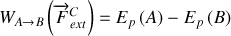
ce qui peut encore s'écrire :
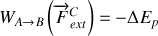
Attention :
La variation d'énergie potentielle entre deux points
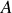et
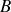est égale à l'opposé du travail de la force conservative entre ces deux points.
Cette relation conduit, en explicitant le travail, à la définition intégrale de l'énergie potentielle:
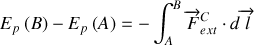
De l'expression intégrale, on peut déduire l'expression différentielle de l'énergie potentielle en faisant apparaître le travail élémentaire de la force conservative soit:
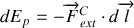
En écrivant la différentielle de l'énergie potentielle en fonction du gradient de Ep:
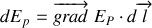
On aboutit à la forme locale de l'énergie potentielle:
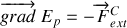
Ces trois formes sont équivalentes entre elles comme l'indique le schéma récapitulatif ci joint.
