Considérons un oscillateur harmonique horizontal constitué d'une masse
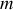et d'un ressort
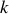pour lequel une force de frottement solide est appliquée à la masse
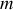(figure 11).
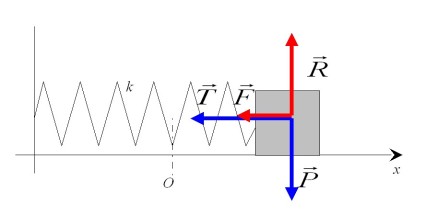
L'application de la RFD au système masse
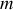conduit à:
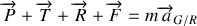
Nous supposons que la force de frottement solide est constante tout au cours du mouvement de l'oscillateur et égale en intensité à
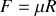. Par projection de la RFD sur l'axe des abscisses, nous obtenons l'équation différentielle du mouvement qui s'écrit:
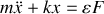
avec
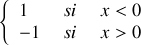
Remarque :
L'équation différentielle du mouvement de
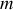change à chaque fois que
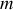passe par une position d'arrêt ce qui oblige à un peu de prudence dans la méthode de résolution. En effet cela revient à résoudre l'équation différentielle par morceaux en respectant la continuité de
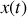entre chaque morceaux.
Nous supposons que la masse
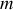est à la position
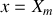au temps
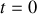et qu'elle a une vitesse nulle à
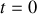. L'équation différentielle est du deuxième ordre à second membre constant. Nous utiliserons donc la même méthode que pour une équation du premier ordre à second membre constant (voir le grain "Lois de conservation").
Nous séparons le mouvement en différents tronçons correspondants au passage de la masse
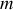par des positions extrémales (vitesse nulle). Nous ferons l'hypothèse que le premier tronçon s'effectue à vitesse négative (mouvement de droite à gauche) ce qui conduit à une équation différentielle du type:
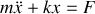
La somme de la solution particulière et de la solution de l'équation sans second membre est une solution générale de cette équation et s'écrit:
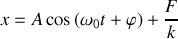
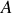et
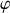sont déterminés par les conditions initiales du mouvement qui conduisent à:
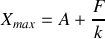et
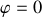
Sur le premier tronçon nous avons donc:
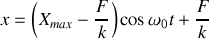
Sur le second tronçon la vitesse est ensuite positive et la masse
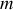quitte sa position de départ donnée par:
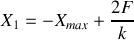
avec une vitesse nulle. L'équation différentielle du mouvement sur ce tronçon s'écrit:
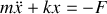
Il faut alors à nouveau résoudre cette nouvelle équation différentielle sur ce tronçon en tenant compte des nouvelles conditions initiales. Il est facile de voir que la solution générale s'écrit:
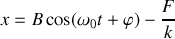
A
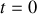, nous avons
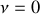et
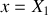ce qui permet de déterminer
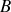et
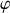. La solution s'écrit alors:
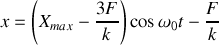
Il est possible de déterminer l'équation horaire sur chaque tronçon en poursuivant ce raisonnement. Une forme générale de la solution peut s'écrire:
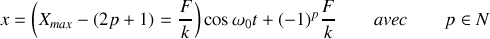
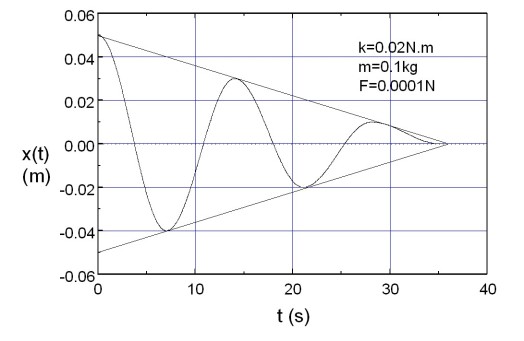
Nous présentons sur la figure 12 le graphe de
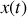pour un oscillateur amorti par frottement solide. Nous observons que l'amplitude des oscillations décroît linéairement au cours du temps ce que l'on pouvait prévoir en observant qu'à chaque fois que le temps
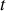s'accroît d'une période propre
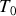l'amplitude décroît de
.
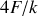Une autre façon très élégante de résoudre ce problème est d'utiliser l'approche énergétique. L'oscillateur étant amorti l'énergie mécanique ne se conserve pas et décroît progressivement au cours du temps. La variation d'énergie mécanique est égale au travail de la force de frottement entre deux positions de l'oscillateur. Il convient comme précédemment de raisonner sur les tronçons à vitesse positive ou négative. La force de frottement étant constante, le travail de cette force varie linéairement avec la position de l'oscillateur. Ainsi sur le premier tronçon, la variation d'énergie mécanique entre le point de départ
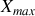et un point
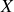quelconque est donnée par:
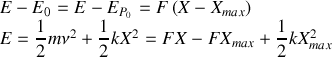
La position d'arrêt
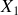de l'oscillateur sur ce tronçon est obtenue en exprimant que l'énergie cinétique de l'oscillateur en
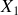est nulle soit:
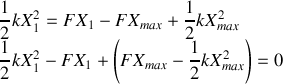
Remarque :
Il est facile de voir que la position
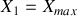est solution de cette équation du second degré ce qui correspond au point de départ de l'oscillateur pour lequel l'énergie cinétique est également nulle. L'autre solution de cette équation est:
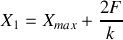
Nous pouvons ainsi obtenir analytiquement toutes les positions d'arrêt de l'oscillateur. En outre, une solution graphique est également possible comme le montre la figure 13.
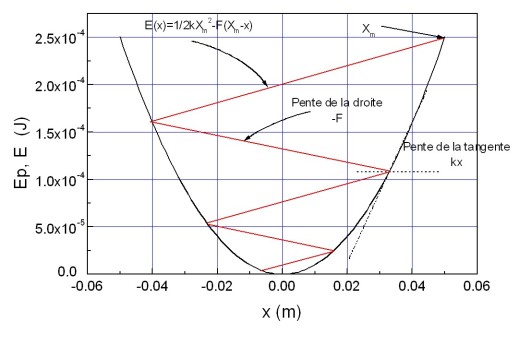
Les positions d'arrêt correspondent aux intersections de la courbe
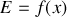avec
.
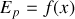Remarque :
La position d'arrêt définitive de l'oscillateur peut être appréhendée. En effet cette position d'arrêt est obtenue lorsque la tension du ressort devient égale à la force de frottement solide. La tension du ressort est, au signe près, égale à la dérivée de l'énergie potentielle élastique. Graphiquement elle est représentée en tout points par la pente de la tangente à la courbe
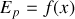. Il y aura donc arrêt définitif lorsque la pente de la tangente à la courbe
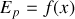sera égale à la pente des droites
.
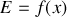Remarque :
Il existe deux différences notables entre l'oscillateur harmonique à frottement solide et l'oscillateur harmonique à frottement visqueux. Pour un frottement solide la période des oscillations ne dépend par de la force de frottement, l'amplitude maximale des oscillations (positions d'arrêt) décroît linéairement et la position d'arrêt définitif ne correspond pas généralement à celle d'équilibre de l'oscillateur sans frottement. Pour un oscillateur à frottement visqueux, l'amplitude maximale décroît exponentiellement, la pseudopériode diffère de la période propre
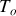et l'arrêt se fait nécessairement à l'équilibre de l'oscillateur sans frottement.
Toutes ces remarques s'observent facilement d'un point de vue expérimental.
