Rappelons que le potentiel vecteur obéit dans les conditions de jauge convenable à une équation de Poisson analogue à celle de l'électrostatique

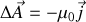
et que donc par analogie avec le champ électrique créé par une distribution de charges

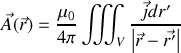
ou en passant à l'intensité électrique, en supposant 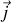constant sur un circuit 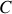d'élément de longueur

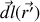
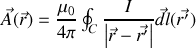
(formule qui redonne bien celle de Biot et Savart si on en prend le rotationnel).

Si on applique la deuxième formule du gradient qui dit que 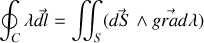pour toute surface 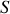s'appuyant sur

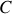
(formule obtenue en multipliant scalairement à gauche par un vecteur \vec{a} constant puis en appliquant la formule de Stokes et celle du produit mixte, sachant que :

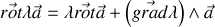
avec cette formule du gradient, donc, il vient

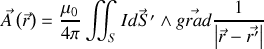
et en développant l'expression du gradient

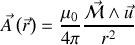
en utilisant l'approximation du circuit élémentaire, avec 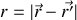distance entre ce circuit à la position 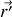et le point 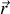où le potentiel vecteur est calculé, et 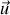vecteur unitaire de ce même vecteur 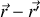en prenant garde au signe lors du calcul du gradient.

Cette dernière formule, élégante, est à rapprocher de celle donnant le potentiel électrostatique créé par un dipôle électrique.

En supposant que 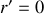(dipôle à l'origine du repère des sphériques) et en supposant que 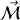est orienté suivant l'axe 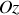, ce que nous pouvons toujours faire, il est alors facile d'établir :

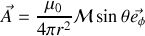
puis de prendre le rotationnel de cette expression pour trouver

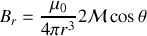
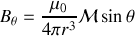
ou sous une forme plus compacte

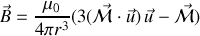
formule à rapprocher du résultat obtenu en électrostatique.