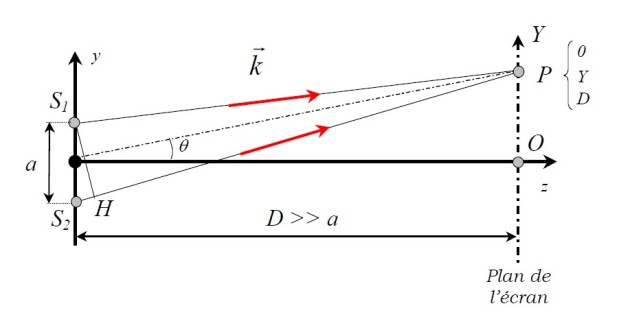
Expression de l'intensité
Nous allons considérer le cas de deux ondes isochrones de même état de polarisation. Ces deux ondes proviennent de deux sources
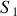 et
et
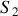 et parviennent au point
et parviennent au point
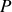 ou elles se superposent.
ou elles se superposent.
Les ondes lumineuses provenant de
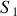 et de
et de
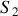 ont pour expression en
ont pour expression en
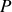 :
:
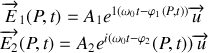
Il en résulte que le champ résultant en
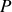 est la somme vectorielle de ces deux champs et s'écrit :
est la somme vectorielle de ces deux champs et s'écrit :
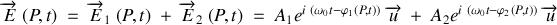
Ce champ a le même état de polarisation que les deux champs incidents. On peut ainsi constater que la polarisation peut donc être omise et que les champs électriques peuvent être assimilés dans un tel cas à des champs vibratoires scalaires.
Le carré du module du champ résultant est donc donné par :
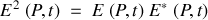
Ce qui conduit à :
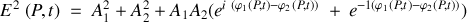
En appelant
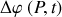 la différence de phase entre les deux ondes on voit que le module au carré du champ résultant en
la différence de phase entre les deux ondes on voit que le module au carré du champ résultant en
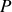 s'écrit :
s'écrit :
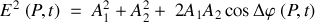
Les deux ondes provenant des deux sources
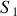 et
et
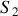 interfèrent en
interfèrent en
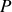 et conduisent à un champ résultant qui peut varier en fonction de la différence de phase entre les deux ondes issues de
et conduisent à un champ résultant qui peut varier en fonction de la différence de phase entre les deux ondes issues de
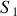 et de
et de
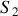 . Lorsque les deux ondes arrivent en phase au point
. Lorsque les deux ondes arrivent en phase au point
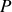 l'amplitude du champ est maximale et vaut
l'amplitude du champ est maximale et vaut
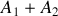 . Si elles arrivent en opposition de phase en
. Si elles arrivent en opposition de phase en
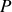 l'amplitude du champ est minimale et vaut
l'amplitude du champ est minimale et vaut
 .
.
Remarque :
De façon générale l'intensité lumineuse qui est proportionnelle au carré du module du champ est susceptible de fluctuer avec la différence de phase des deux ondes incidentes.
L'intensité que l'on mesure à l'aide d'un détecteur est intégrée sur le temps de réponse du détecteur ce qui équivaut à faire la moyenne temporelle du carré du module du champ soit :
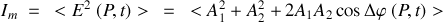
Dans cette expression, les crochets signifient que l'on réalise la moyenne de cette quantité sur l'intervalle de temps de mesure soit :
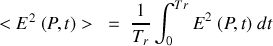
La moyenne d'une somme étant la somme des moyennes nous obtenons :
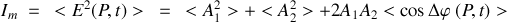
ce qui entraîne
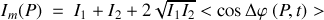
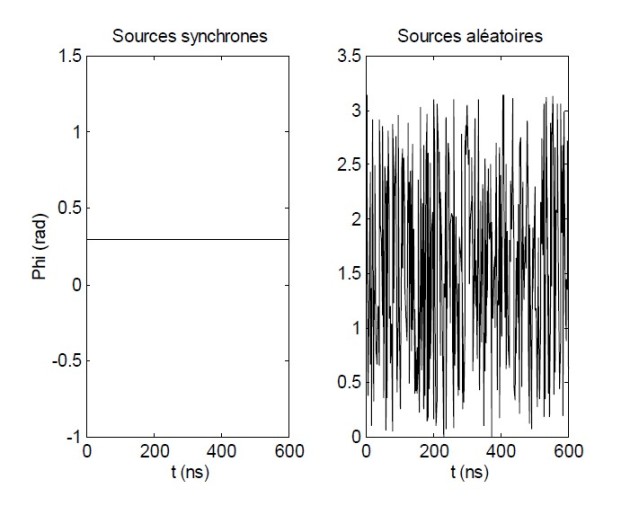
Nous voyons donc que l'intensité résultant de la superposition de deux ondes dépend essentiellement de la valeur moyenne des fluctuations temporelles de la phase entre les deux ondes. Il y aura possibilité de voir des interférences entre les deux ondes si les fluctuations de phase ne varient pas aléatoirement dans le temps ce qui impose de disposer de sources synchrones.
Pour deux sources incohérentes, la différence de phase entre les deux sources varie continuellement dans le temps entre
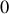 et
et
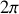 . Les ondes issues des deux sources seront donc incohérentes entre elles après s'être propagées et
. Les ondes issues des deux sources seront donc incohérentes entre elles après s'être propagées et
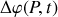 sera donc une variable aléatoire. Il en résulte que le cosinus de cet angle varie entre 1 et -1 et qu'en moyenne dans le temps il vaut
sera donc une variable aléatoire. Il en résulte que le cosinus de cet angle varie entre 1 et -1 et qu'en moyenne dans le temps il vaut
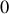 . Pour des sources incohérentes, l'intensité détectée est donc :
. Pour des sources incohérentes, l'intensité détectée est donc :
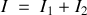
c'est à dire la somme des intensités provenant de chaque ondes.
Nous retiendrons donc que :
Attention :
La superposition de deux ondes lumineuses issues de deux sources incohérentes produit sur un écran une intensité uniforme égale à la somme des intensités de ces deux ondes
Si les sources sont synchrones la différence de phase est constante au cours du temps et la moyenne temporelle du cosinus est égale à :
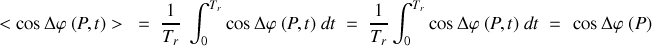
Il en résulte que l'intensité mesurée n'est plus la somme des intensités de chaque onde mais :
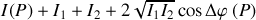 (1)
(1)
Nous retiendrons donc que :
Attention :
L'intensité issue de la superposition de deux ondes cohérentes n'est pas uniforme mais présente des maxima et minima d'intensité appelés franges d'interférences. L'intensité au point P s'obtient en calculant le module au carré de la somme des amplitudes complexes en
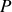 .
.
Nous allons maintenant étudier ce que l'on peut attendre de l'équation (1)
Conséquences
Nous venons de montrer que la superposition de deux ondes produit une intensité régie par l'équation (1)
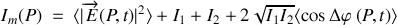
Il nous faut maintenant exprimer la différence de phase entre les ondes arrivant en
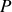 à l'instant
à l'instant
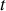 . Cette différence de phase est la somme d'une différence de phase due à la propagation des ondes et d'une éventuelle différence de phase due à l'incohérence des sources.
. Cette différence de phase est la somme d'une différence de phase due à la propagation des ondes et d'une éventuelle différence de phase due à l'incohérence des sources.
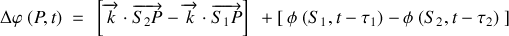
Supposons que les ondes soient synchrones à la source, alors
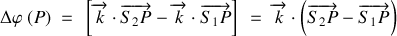
Si les deux sources ont même intensité, l'intensité en
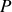 devient
devient
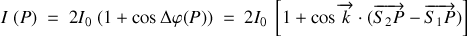
Pour des ondes planes se propageant dans la direction de l'axe
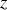 nous avons
nous avons
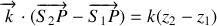
ce qui conduit à
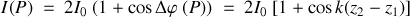
Remarque :
L'intensité en
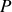 ne dépend alors que de la différence de trajet parcourue par les deux ondes pour aller de
ne dépend alors que de la différence de trajet parcourue par les deux ondes pour aller de
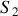 ou
ou
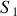 en
en
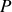 . Cette différence de trajet est appelée tout naturellement la différence de marche et est notée
. Cette différence de trajet est appelée tout naturellement la différence de marche et est notée
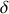 . Nous voyons ainsi que la différence de phase entre les deux ondes arrivant au point
. Nous voyons ainsi que la différence de phase entre les deux ondes arrivant au point
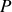 s'exprime par
s'exprime par
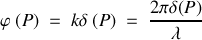
ce qui conduit à
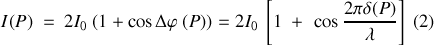
L'équation (2) montre que selon la valeur de la différence de marche
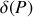 , l'intensité mesurée en
, l'intensité mesurée en
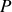 peut être aussi bien :
peut être aussi bien :
nulle si
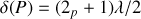 car dans ce cas
car dans ce cas
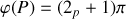 et les ondes arrivent en
et les ondes arrivent en
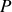 en opposition de phase
en opposition de phase
maximale et égale à
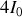 si
si
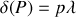 car dans ce cas
car dans ce cas
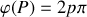 et les ondes arrivent en phase en
et les ondes arrivent en phase en
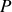 .
.
Dans le premier cas nous dirons que les ondes interfèrent de façon destructive en
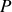 alors que dans le second cas elles interfèrent de façon constructive.
alors que dans le second cas elles interfèrent de façon constructive.
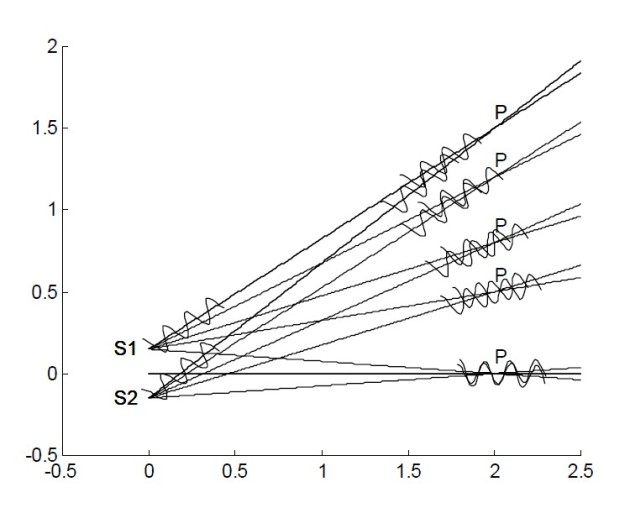
Représentation schématique de la superposition de deux ondes en différents points
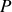 d'un écran. Selon la position de ce point les ondes issues des sources
d'un écran. Selon la position de ce point les ondes issues des sources
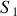 et
et
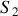 arrivent en phase, en opposition de phase, en quadrature ou déphasées de façon quelconque en
arrivent en phase, en opposition de phase, en quadrature ou déphasées de façon quelconque en
 .
.
Il apparaît ainsi une propriété remarquable de cette approche qui est la suivante :
Propriété :
La superposition de deux ondes lumineuses synchrones peut soit produire de l'obscurité soit une intensité lumineuse supérieure à la somme des intensités de chaque source.
Cette propriété peu banale constitue le phénomène d'interférences lumineuses. L'observation expérimentale d'un tel phénomène prouve la nature ondulatoire de la lumière. En d'autres termes, si la lumière est bien une onde nous devons donc pouvoir le vérifier expérimentalement en réalisant des interférences.
Il faut rendre hommage ici à Young et à Fresnel qui au 19ème siècle ont mis pour la première fois en évidence la nature ondulatoire de la lumière. Newton avait au 17ème siècle réfuté cette hypothèse et il était admis par la communauté scientifique de l'époque que la lumière avait une nature corpusculaire plutôt qu'ondulatoire. Nous allons voir maintenant comment Young s'y est pris pour mettre en évidence le phénomène des interférences lumineuses.