On démontre que toute fonction
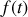 , périodique de période
, périodique de période
 et satisfaisant à certaines conditions de continuité et de dérivabilité, peut se décomposer en une somme de fonctions sinusoïdales dite « série de
Fourier
» :
et satisfaisant à certaines conditions de continuité et de dérivabilité, peut se décomposer en une somme de fonctions sinusoïdales dite « série de
Fourier
» :
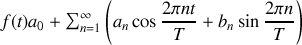
Avec :


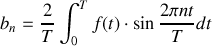

A titre d'exemple, on a représenté les trois premiers termes du développement en série de Fourier d'une fonction triangle :

La convergence est assez rapide. Pour la fonction créneau, représentée par :

la convergence est par contre très lente.
La réponse d'un système linéaire à une fonction périodique est la somme des réponses aux fonctions sinusoïdales constituant le développement en série de Fourier de cette fonction. En conséquence, on peut privilégier l'étude de la réponse des circuits à une excitation sinusoïdale. La réponse à une fonction périodique sera obtenue en faisant la somme des réponses du circuit aux différents termes (nommés harmoniques) de sa décomposition en série de Fourier.
Cliquez ici pour visualiser d'autres décompositions de signaux en série de Fourier.
D'autre part, pour des raisons économiques et pratiques, l'énergie électrique est distribuée sous la forme de courants sinusoïdaux (de fréquence
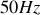 ). En effet, les pertes liées au transport sont proportionnelles au carré de l'intensité : pour les diminuer il faut donc, à puissance constante, augmenter la tension. Or il existe un dispositif, le transformateur, qui permet de modifier avec des pertes faibles la tension d'un courant variable dans le temps.
). En effet, les pertes liées au transport sont proportionnelles au carré de l'intensité : pour les diminuer il faut donc, à puissance constante, augmenter la tension. Or il existe un dispositif, le transformateur, qui permet de modifier avec des pertes faibles la tension d'un courant variable dans le temps.
Remarque :
Dans les centrales électriques, on utilise comme générateurs des alternateurs (machines tournantes) qui délivrent une tension sinusoïdale. Des transformateurs élèvent la tension de transport à quelques centaines de milliers de volts. Au voisinage des utilisateurs, d'autres transformateurs abaissent la tension à des valeurs permettant une exploitation sans danger.
Pour les applications qui nécessitent une tension continue, on procède à la transformation du courant alternatif en un courant continu.
Cliquez ici pour analyser le problème du transport de l'énergie électrique.




