On recherche les conditions de transmission optimale de la puissance entre un générateur modélisé par un générateur idéal en série avec une impédance
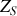et une charge d'impédance
.
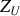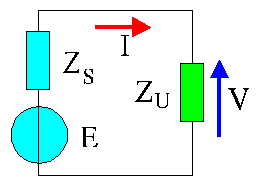
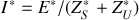
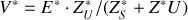
La puissance active est donc :
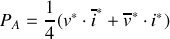
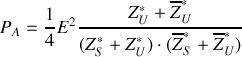
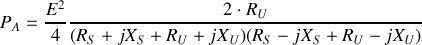
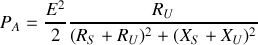
La puissance est maximale si le dénominateur est minimal.
Ceci est obtenu en faisant :
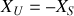. On rappelle que si une résistance est toujours positive, une réactance peut être positive ou négative.
L'expression de la puissance est alors uniquement fonction de
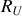et
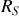. La puissance sera maximale si :
.
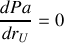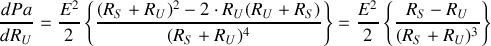
Cette dérivée s'annule si
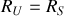. En tenant compte de la condition sur les réactances, on obtient donc une transmission de puissance optimale si l'impédance de la charge est le complexe conjugué de celle de la source. Quand cette condition est réalisée, il y a adaptation des impédances en puissance.
Pour un circuit alimenté en courant continu les impédances sont réelles et la transmission de puissance est optimale quand la résistance du récepteur est égale à celle de la source.
On peut noter que lorsque les impédances sont adaptées, la puissance perdue dans l'impédance de source est égale à la puissance utilisable dans la charge.
Remarque :
La condition obtenue correspond à une adaptation des puissances. Si l'on souhaite par contre obtenir une tension maximale entre les bornes de la charge, puisque
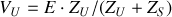), il faut évidemment que l'impédance de cette charge soit la plus grande possible et que l'impédance de la source soit la plus petite possible. On réalise alors une adaptation d'impédance en tension.
