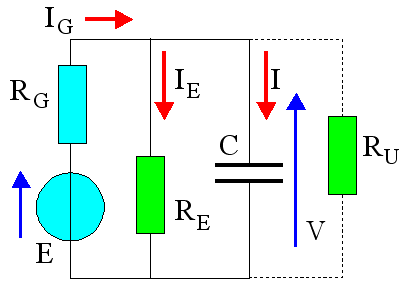
On se place dans le cas le plus général :
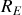est une résistance qui tient compte de la résistance de fuite du condensateur
et de la résistance de charge éventuelle
. (
).
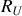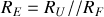Le générateur utilisé pour la charge est modélisé par un générateur idéal de f.e.m.
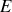et de résistance interne
.
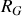Méthode des mailles
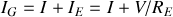
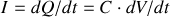
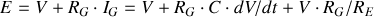
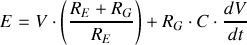
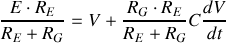
Donc en posant :
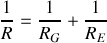, on tire
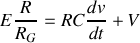
Méthode de Thévenin
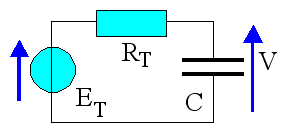
Le générateur équivalent qui est relié au condensateur est caractérisé par :
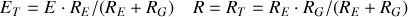
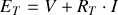
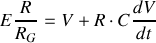
La solution générale de l'équation sans second membre est :
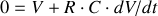
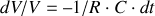
Si
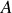désigne une constante arbitraire, la solution de cette équation (1er ordre) est :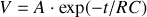
Comme une quantité d'électricité est le produit d'une capacité par une tension, en utilisant les équations dites « aux dimensions » , on tire :
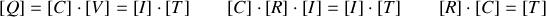
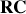qui a la dimension d'un temps est la « constante de temps »
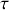du circuit.
Solution particulière de l'équation avec second membre :
Si
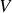est constant alors
.
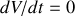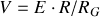est donc une solution. Elle correspond au régime permanent : la charge du condensateur est alors terminée.
Solution complète de l'équation différentielle :
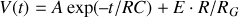
Solution physique de l'équation différentielle :
Pour obtenir la solution du problème physique, il faut préciser les conditions initiales de celui-ci. Si l'on suppose le condensateur totalement déchargé lors de la mise sous tension du montage : en
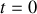, on a alors
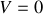.La valeur de la constante
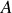est donc :
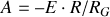. On en déduit :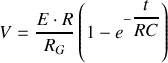
La durée nécessaire à la charge totale est donc infinie. En pratique, cherchons au bout de combien de temps la charge atteint sa valeur finale à un millième près : si
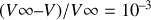alors :
.
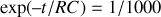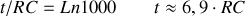
Au bout de
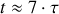, la charge ne diffère de la charge finale que de 0,001. On peut considérer la charge du condensateur terminée.
Graphes de la tension V et des divers courants
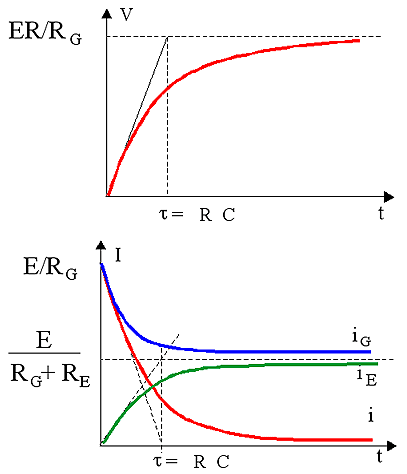
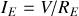
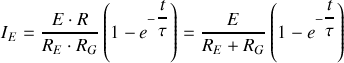
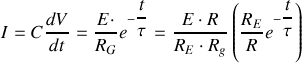
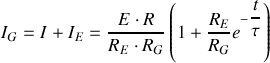
Bien noter sur ces graphiques les valeurs limites des tensions et courants et les valeurs des pentes des tangentes à l'origine.
Remarque :
Un condensateur déchargé se comporte au début de la charge comme un courtcircuit pour l'alimentation. Seule la résistance
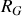limite alors la valeur du courant.
