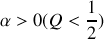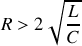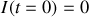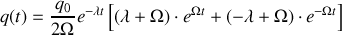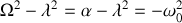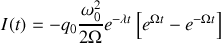Le condensateur
du circuit
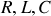suivant est chargé par un générateur auxiliaire qui est ensuite déconnecté par
.
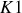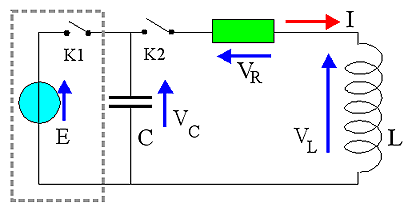
La charge initiale du condensateur est :
Si
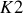est fermé et
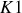ouvert, on a :
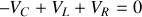
On obtient l'équation :
On pose :
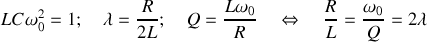
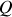est le facteur de qualité et
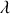le facteur d'amortissement.
L'équation devient :
En cherchant des solutions de la forme
, on obtient l'équation dite « équation caractéristique » suivante :
Ses racines sont :
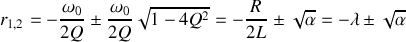
La solution générale de l'équation est de la forme :
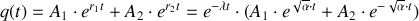
La constante de temps est ici :
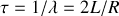. Il faut connaître deux conditions initiales
Selon le signe de
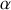, la nature des solutions diffère.
Amortissement fort
ou
Les deux racines sont réelles. On pose :
Les conditions initiales sont
et
On tire :
Comme
, on obtient :
Ce régime de fonctionnement est le régime apériodique. Le système revient à son état d'équilibre
sans oscillations.
Exercice
Montrer que
Amortissement critique
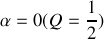
Il y a une racine double
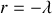
La solution générale est de la forme :
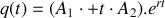
Avec les conditions initiales précédentes, on obtient :
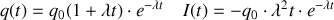
Le régime de fonctionnement est apériodique et critique. C'est un régime limite qui est obtenu en diminuant la valeur de
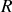jusqu'à la valeur
.
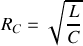Amortissement faible
ou
On pose
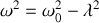. Les deux racines sont imaginaires conjuguées et valent :
Toujours avec les mêmes conditions initiales
, on obtient :
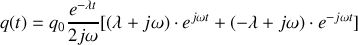
Et en posant
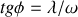et donc
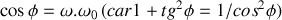, on a :
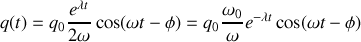
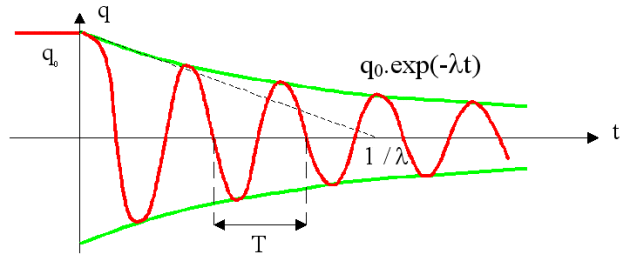
On obtient un régime oscillant amorti « pseudopériodique » (à cause de l'amortissement le phénomène n'est pas exactement répétitif) caractérisé par une pseudopériode
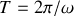et par le terme d'amortissement
.
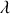Amortissement nul
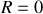
L'équation se résume à :
Le régime est sinusoïdal (périodique, non amorti). La période est :
.
Cliquez ici pour tester le fonctionnement du circuit RLC série en régime libre.
