Les composants utilisés en électronique sont très souvent non linéaires et une étude analytique rigoureuse du circuit est alors impossible. Pour étudier le comportement du circuit, on peut utiliser des méthodes graphiques.
Supposons connues les caractéristiques d'un quadripôle non linéaire : ce sont les réseaux de courbes
et
.
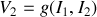Exemple :
Dans le plan
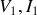on trace le réseau des courbes
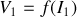en prenant la valeur du courant
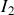comme paramètre. De même dans le plan
,
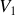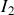, on trace le réseau des courbes
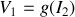en prenant la valeur de
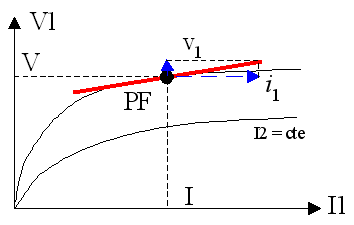
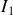comme paramètre. On impose à l'entrée les valeurs de
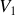et de
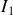; les valeurs de sortie sont
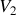et
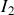. Ces 4 valeurs définissent le point de repos ou point de fonctionnement. Comment évolue ce point si
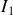varie de
?
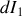Au voisinage du point de repos, on peut écrire les variation des valeurs « statiques » :
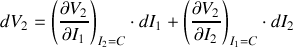
Les dérivées partielles
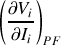sont les pentes des tangentes aux caractéristiques au voisinage du point de repos et ont la dimension d'une impédance :
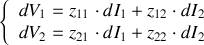
Les paramètres
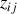sont les dérivées des paramètres « statiques »
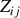au voisinage du point de repos : ce sont des paramètres « dynamiques ». Cette notation des différentielles est rigoureuse mais lourde à utiliser.
Attention :
En électronique, on note la différentielle
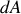de la grandeur
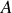avec la lettre minuscule
.
La minuscule a correspond à la variation de la grandeur statique représentée par
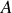. Ainsi, en posant
;
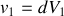... , on obtient pour la matrice impédance :
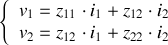
Dans une région où les caractéristiques sont linéaires, ce modèle permet une représentation correcte des propriétés du quadripôle. Il est également possible de modéliser le quadripôle par un circuit linéaire équivalent dont les valeurs sont celles du quadripôle au voisinage du point de fonctionnement. Ainsi pour le modèle hybride, on obtient (comparer avec la figure 17) :
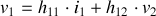
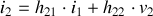
Attention :
Ne pas confondre les
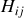et les
.
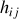