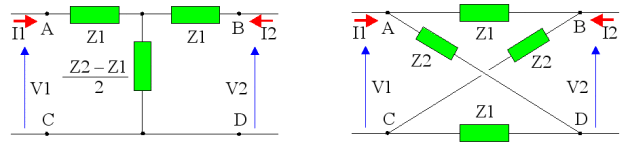
On va montrer que ces deux structures de filtres sont équivalentes en calculant leurs matrices impédances.
Circuit en
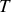 :
:
Le courant qui circule dans l'impédance
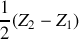 est
est
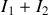 .
.
Dans le circuit d'entrée, on a :
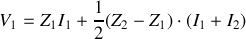 .
.
Dans le circuit de sortie, on a :
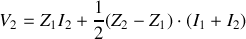 .
.
On tire :
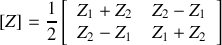
Treillis
Première méthode
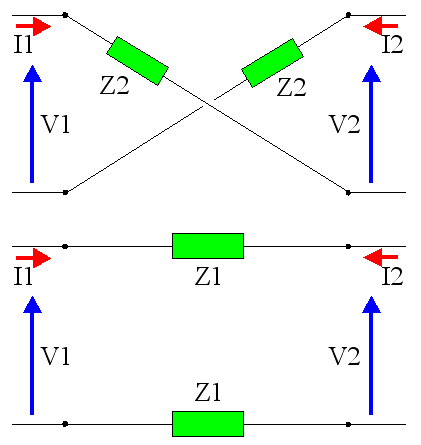
Pour ce quadripôle
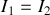 et
et
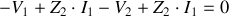
Soit
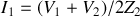 .
.
Et donc :
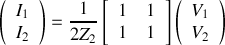
Pour le second quadripôle on a :
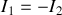 et
et
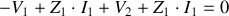
L'expression de sa matrice admittance est :
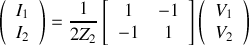
En reliant les deux quadripôles en parallèle, on obtient le treillis. La matrice admittance du treillis est dont égale à la somme des matrices admittances des deux quadripôles associés soit :
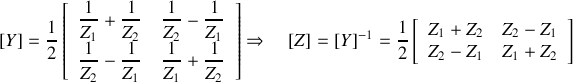
Vérifier que l'expression de la matrice de transferts est :
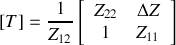
On peut voir sur cet exemple que la méthode matricielle est lourde à utiliser.
Deuxième méthode
On redessine le treillis sous la forme d'un pont.
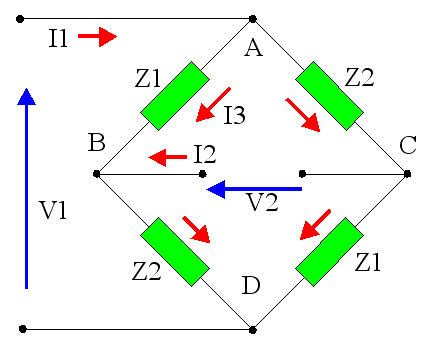
Si
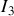 est le courant entre
est le courant entre
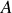 et
et
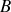 , le courant entre
, le courant entre
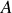 et
et
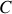 est
est
 , le courant entre
, le courant entre
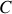 et
et
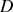 est
est
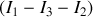 .
.
Entre
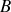 et
et
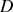 le courant est
le courant est
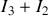 .
.
La ddp entre
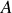 et
et
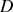 s'écrit :
s'écrit :
(en passant par
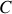 )
)
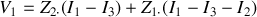
(en passant par
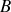 )
)
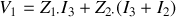
On tire :
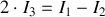
Et :
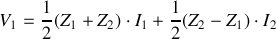
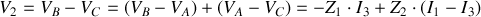
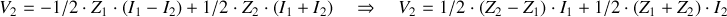
Les deux quadripôles ayant la même matrice impédance sont équivalents.