Énoncé
Un mobile de masse
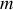 est dans un ascenseur se déplaçant verticalement par rapport à un référentiel
est dans un ascenseur se déplaçant verticalement par rapport à un référentiel
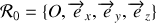 supposé galiléen.
supposé galiléen.
On résonnera en travaillant dans le référentiel non galiléen
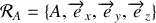 lié au sol de l'ascenseur. L'axe
lié au sol de l'ascenseur. L'axe
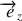 est pris dans le sens de la verticale ascendante.
est pris dans le sens de la verticale ascendante.
Déterminer la force de contact de l'ascenseur sur le mobile.
En déduire la condition sur le mouvement de l'ascenseur pour éviter que le mobile ne décolle du sol de l'ascenseur.
Déterminer la position du mobile dans le référentiel
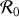 lié au sol.
lié au sol.Déterminer l'accélération du mobile par rapport à
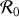 puis par rapport à
puis par rapport à
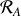 .
.Faire le bilan des forces s'appliquant sur le mobile.
Appliquer le principe fondamental de la dynamique dans le repère galiléen
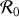 .
.En déduire l'expression du principe fondamental de la dynamique dans le repère non galiléen
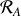 .
.
1. En appelant
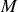 la position du centre de gravité du mobile, le vecteur position du mobile dans le repère
la position du centre de gravité du mobile, le vecteur position du mobile dans le repère
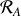 est :
est :
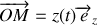 . Il peut être décomposé en utilisant le centre
. Il peut être décomposé en utilisant le centre
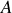 du repère
du repère
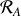 lié à l'ascenseur :
lié à l'ascenseur :
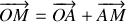 , faisant ainsi apparaître le vecteur position
, faisant ainsi apparaître le vecteur position
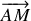 du mobile dans le repère
du mobile dans le repère
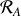 et le vecteur position de l'ascenseur
et le vecteur position de l'ascenseur
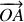 . Le solide étant indéformable, le vecteur
. Le solide étant indéformable, le vecteur
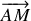 est constant tant que le mobile ne décolle pas du sol de l'ascenseur.
est constant tant que le mobile ne décolle pas du sol de l'ascenseur.
On obtient l'accélération en dérivant deux fois le vecteur position dans le repère choisi. Ainsi l'accélération du mobile par rapport au référentiel
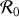 est
est
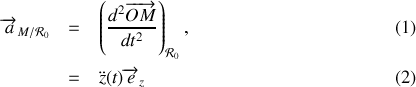 .
.
Alors que l'accélération du mobile par rapport au référentiel
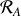 est quant à elle :
est quant à elle :
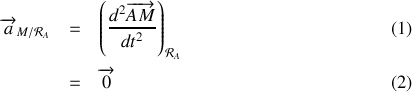
puisque le vecteur
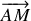 est constant tant que le mobile reste collé au sol.
est constant tant que le mobile reste collé au sol.
Remarque :
Remarquons que si le mobile reste collé au sol de l'ascenseur, alors le mobile et l'ascenseur ont la même accélération.
En effet,
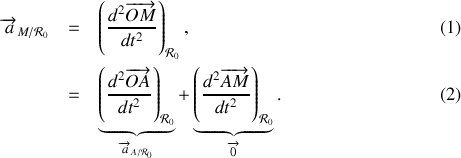
En l'absence de rotation, la composition des accélérations s'écrit donc simplement :
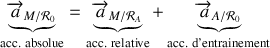
Bilan des forces agissant sur le mobile
Il y a deux forces extérieures s'appliquant sur le mobile :
Le Poids
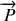 dû à l'interaction gravitationnelle entre le mobile et la Terre. Le poids est vertical descendant et de module
dû à l'interaction gravitationnelle entre le mobile et la Terre. Le poids est vertical descendant et de module
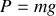 où
où
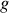 est l'accélération de la pesanteur (supposée ici constante), soit finalement
est l'accélération de la pesanteur (supposée ici constante), soit finalement
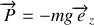 .
.La réaction
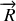 de l'ascenseur sur le mobile. La réaction est verticale ascendante strictement :
de l'ascenseur sur le mobile. La réaction est verticale ascendante strictement :
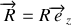 avec
avec
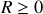 .
.
Application du principe fondamental de la dynamique dans
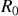
Le repère
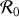 étant galiléen, on peut appliquer le principe fondamental de la dynamique stipulant que la somme des forces extérieures s'appliquant sur le mobile
étant galiléen, on peut appliquer le principe fondamental de la dynamique stipulant que la somme des forces extérieures s'appliquant sur le mobile
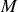 est égale au produit de sa masse et de son accélération par rapport au repère galiléen
est égale au produit de sa masse et de son accélération par rapport au repère galiléen
 soit :
soit :

L'égalité vectorielle (7) n'a qu'une seule composante non nulle sur l'axe
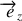 ; elle est équivalente à l'égalité scalaire issue de sa projection dans la direction
; elle est équivalente à l'égalité scalaire issue de sa projection dans la direction
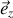 soit
soit
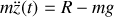
Application du principe fondamental de la dynamique dans
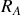
Pour appliquer le principe fondamental de la dynamique dans le repère
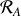 non-galiléen, il faut ajouter aux forces extérieures déjà déterminées
non-galiléen, il faut ajouter aux forces extérieures déjà déterminées
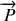 et
et
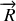 , la force d'inertie issue du mouvement d'entraînement de l'ascenseur :
, la force d'inertie issue du mouvement d'entraînement de l'ascenseur :
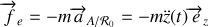 . Le principe fondamental de la dynamique nous affirme alors que la somme des forces extérieures s'appliquant sur le mobile
. Le principe fondamental de la dynamique nous affirme alors que la somme des forces extérieures s'appliquant sur le mobile
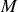 , augmentée des forces d'inertie, est égale au produit de la masse et de l'accélération du mobile par rapport au repère non galiléen
, augmentée des forces d'inertie, est égale au produit de la masse et de l'accélération du mobile par rapport au repère non galiléen
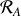 ; soit
; soit
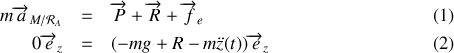
Encore une fois, cette équation vectorielle se ramène à l'équation scalaire
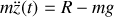
par projection dans la direction
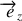 .
.
2. Analyse de l'équation du mouvement
Remarquons tout d'abord que tant que le mobile reste collé au sol de l'ascenseur, la grandeur
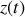 n'est pas une variable mais un paramètre puisqu'elle correspond à l'accélération de l'ascenseur qui est imposée de l'extérieur.
n'est pas une variable mais un paramètre puisqu'elle correspond à l'accélération de l'ascenseur qui est imposée de l'extérieur.
Ainsi, la seule inconnue du problème est ici la force de réaction de l'ascenseur sur le mobile
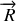 qui nous est donnée par l'équation du mouvement.
qui nous est donnée par l'équation du mouvement.
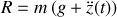
Lorsque l'ascenseur se déplace à vitesse constante
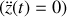 , la réaction compense le poids du mobile
, la réaction compense le poids du mobile
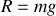 .
.
Si l'ascenseur accélère
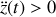 la réaction augmente
la réaction augmente
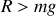 , ce qui est à l'origine de la sensation d'écrasement au démarrage de l'ascenseur.
, ce qui est à l'origine de la sensation d'écrasement au démarrage de l'ascenseur.
À l'opposé, si l'ascenseur décélère
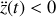 la réaction diminue
la réaction diminue
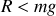 , ce qui est à l'origine de la sensation de légèreté à l'arrivée de l'ascenseur.
, ce qui est à l'origine de la sensation de légèreté à l'arrivée de l'ascenseur.
L'analyse précédente est valable tant que le mobile reste collé au sol de l'ascenseur, c'est-à-dire tant que la réaction
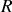 est positive.
est positive.
La condition de décollement est l'annulation de la force de réaction, ce qui se produit lorsque l'accélération de l'ascenseur est égale en norme à l'accélération de la pesanteur :
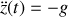 .
.
Dans ce cas, il faut reprendre l'analyse précédente en considérant une accélération relative non nulle.



