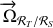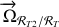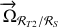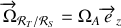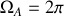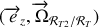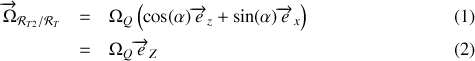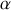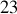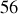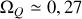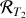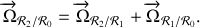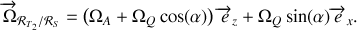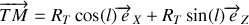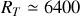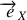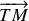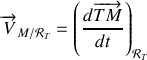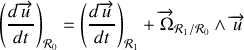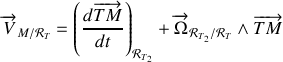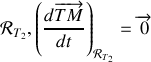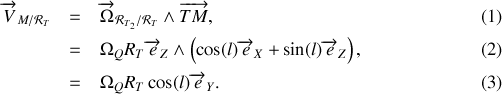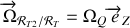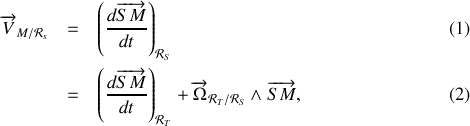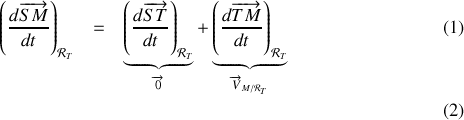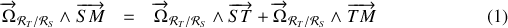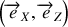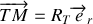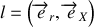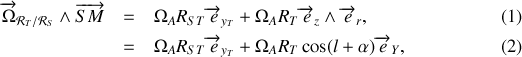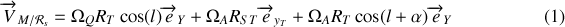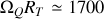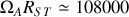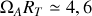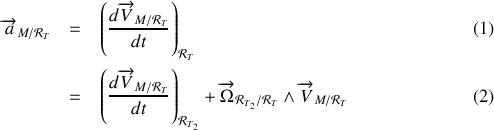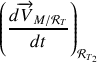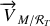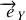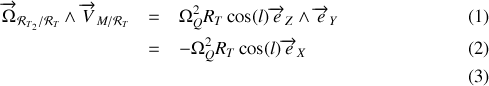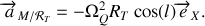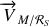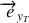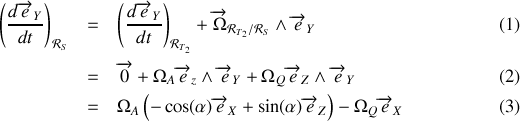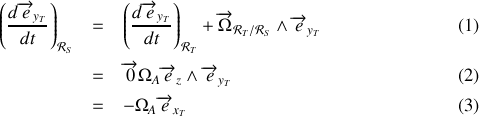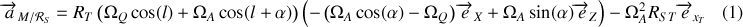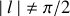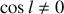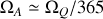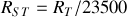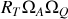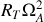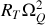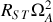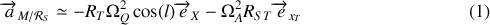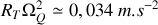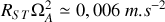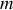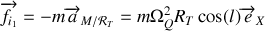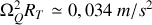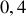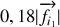1. Révolution annuelle
Le vecteur rotation
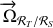 est porté par l'axe
est porté par l'axe
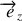 :
:
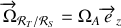 . La Terre effectuant une révolution en 1 an,
. La Terre effectuant une révolution en 1 an,
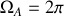 ~rad/an.
~rad/an.
Révolution quotidienne
Il est commode de choisir la direction
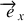 dans le plan :
dans le plan :
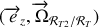 ainsi
ainsi
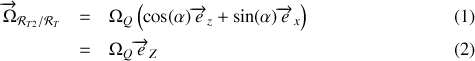 où
où
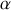 est l'angle entre l'axe de rotation et
est l'angle entre l'axe de rotation et
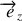 . La Terre effectuant une rotation sur elle-même en
. La Terre effectuant une rotation sur elle-même en
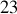 h~
h~
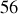 min on a
min on a
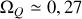 ~rad/h.
~rad/h.
On obtient le vecteur rotation du référentiel
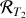 par rapport au référentiel
par rapport au référentiel
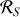 en utilisant la composition des vecteurs rotations:
en utilisant la composition des vecteurs rotations:
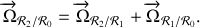
Soit ici :
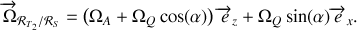
Vitesse d'un point immobile à la surface du globe
La position du point
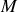 est définit dans le repère
est définit dans le repère
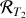 par le vecteur position
par le vecteur position
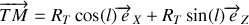 où
où
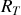 est le rayon terrestre (
est le rayon terrestre (
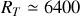 km). On a ici choisi l'axe
km). On a ici choisi l'axe
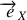 aligné avec la projection de
aligné avec la projection de
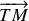 dans le plan équatorial.
dans le plan équatorial.
On obtient ainsi
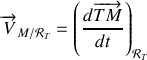
En appliquant la règle de dérivation
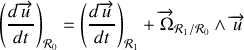
On obtient :
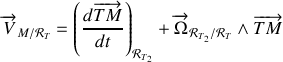 . Le point
. Le point
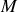 étant immobile par rapport à
étant immobile par rapport à
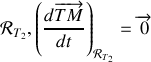 .
.
Soit en effectuant :
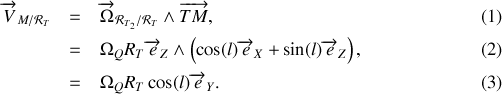
Remarquons que le produit vectoriel est simple à calculer parce que l'on a utiliser la ''bonne'' décomposition du vecteur rotation
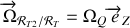 .
.
L'expression de la vitesse par rapport au référentiel
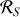 se détermine de la même manière
se détermine de la même manière
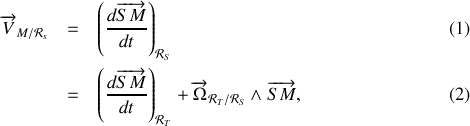
en remarquant que
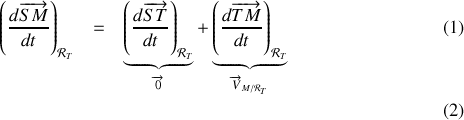
Il reste donc à déterminer le produit vectoriel
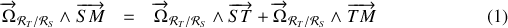
Pour effectuer le second produit scalaire, le plus simple est d'exprimer
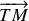 dans un repère polaire du plan
dans un repère polaire du plan
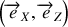 \textit{i.e.}
\textit{i.e.}
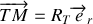 avec l'angle
avec l'angle
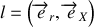 , ainsi
, ainsi
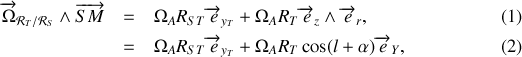
où l'on a introduit la distance
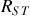 entre le Soleil et la Terre. Finalement on trouve pour la vitesse du point
entre le Soleil et la Terre. Finalement on trouve pour la vitesse du point
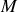 par rapport au référentiel
par rapport au référentiel
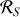
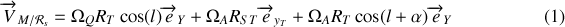
Le premier terme est du à la rotation de la Terre sur elle même et varie avec la latitude, le second est du à la rotation de la Terre autour du Soleil, quant eu troisième il est du à l'inclinaison de l'axe de rotation de la Terre sur elle-même par rapport à l'axe de rotation de la Terre autour du Soleil (terme de couplage).
Il est instructif de donner quelques ordres de grandeur des différents termes. On trouve ainsi que
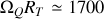 ~km/h,
~km/h,
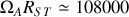 ~km/h et
~km/h et
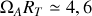 ~km/h. Il apparaît ainsi que le terme de couplage est négligeable et que la principale contribution à la vitesse du point
~km/h. Il apparaît ainsi que le terme de couplage est négligeable et que la principale contribution à la vitesse du point
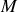 est du à la rotation annuelle de la Terre autour du Soleil
est du à la rotation annuelle de la Terre autour du Soleil
Accélération d'un point immobile à la surface du globe
L'accélération du point
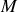 par rapport au référentiel terrestre
par rapport au référentiel terrestre
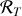 s'obtient en dérivant l'expression de la vitesse :
s'obtient en dérivant l'expression de la vitesse :
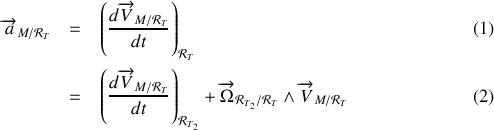
La quantité
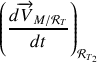 est nulle puisque le vecteur
est nulle puisque le vecteur
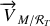 n'a qu'une composante constante porté par
n'a qu'une composante constante porté par
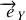 qui est un vecteur fixe par rapport au référentiel
qui est un vecteur fixe par rapport au référentiel
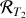 . Quant au produit vectoriel, il se calcul simplement
. Quant au produit vectoriel, il se calcul simplement
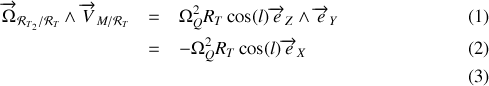
Soit finalement, pour l'accélération du point
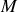 par rapport au référentiel terrestre
par rapport au référentiel terrestre
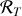 :
:
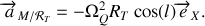
Le calcul de l'accélération de
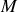 par rapport au référentiel
par rapport au référentiel
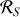 est un peu plus long mais ne pose pas de difficultés particulières. Le vecteur vitesse
est un peu plus long mais ne pose pas de difficultés particulières. Le vecteur vitesse
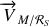 ne comportant que des composantes constante sur
ne comportant que des composantes constante sur
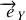 et
et
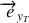 , le calcul de l'accélération revient aux calculs des dérivées de ces deux vecteurs par rapport au référentiel
, le calcul de l'accélération revient aux calculs des dérivées de ces deux vecteurs par rapport au référentiel
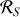 .
.
Soit pour la dérivation de
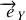
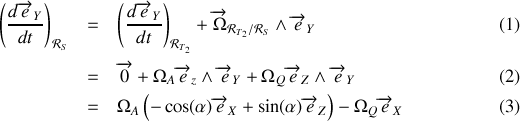
et pour la dérivation de
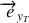
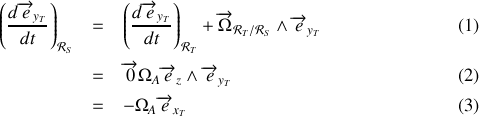
Finalement, on obtient pour l'accélération :
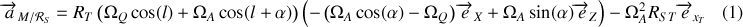
2. Forme approchée de l'accélération
Pour les points éloignés des pôles
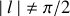 et donc
et donc
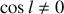 . Or, comme
. Or, comme
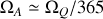 et
et
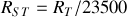 , les termes en
, les termes en
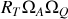 et
et
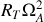 sont négligeables devant ceux en
sont négligeables devant ceux en
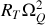 et
et
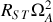 , ce qui conduit à la forme approchée suivante:
, ce qui conduit à la forme approchée suivante:
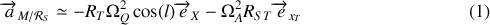
Les deux termes de l'accélération correspondent à la rotation de la Terre sur elle-même pour le premier et à la rotation de la Terre autour du Soleil pour le second.
Il est instructif de comparer les ordres de grandeur de ces deux termes, on trouve que
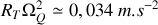 et
et
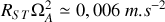 .
.
Il ressort donc que, contrairement au résultat sur la vitesse, le terme dominant de l'accélération est du à la rotation de la Terre sur elle-même.
3. Forces d'inertie
Si le référentiel géocentrique est assimilé à un référentiel galiléen, il faut prendre en compte lors de l'étude mécanique d'un objet de masse
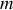 à la surface du globe la force d'inertie
à la surface du globe la force d'inertie
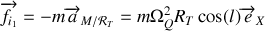 .
.
C'est une force centrifuge dirigée perpendiculairement à l'axe de rotation de la Terre. On peut estimer son importance en la comparant à la force de gravité, on trouve ainsi que
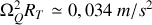 ce qui représente environ
ce qui représente environ
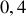 % de l'accélération de la pesanteur.
% de l'accélération de la pesanteur.
Cette force est maximale le long de l'équateur où elle a la direction opposé à celle de la force de gravitation, minimisant ainsi le poids d'un objet. C'est pourquoi les bases spatiales sont placées de préférence à proximité de l'équateur pour minimiser l'énergie nécessaire à la satellisation en "profitant" de la force centrifuge.
Si le référentiel héliocentrique est maintenant assimilé à un référentiel galiléen, une force d'inertie supplémentaire intervient, du à la rotation de la Terre autour du Soleil. C'est aussi une force centrifuge portée par l'axe Terre-Soleil dont le module vaut
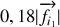 . La force d'inertie résultante est maximale pendant la nuit et minimale le jour.
. La force d'inertie résultante est maximale pendant la nuit et minimale le jour.
La force de pesanteur mesurée à la surface du globe est la résultante de la force d'attraction universelle et des forces d'inertie. Il s'en suit que la verticale d'un lieu indiquée par le fil de plomb ne pointe pas exactement vers le centre de la Terre (ce qui serait le cas en l'absence de force d'inertie).
Remarquons enfin que bien que la vitesse d'un point à la surface du globe soit "astronomique", le fait que son accélération soit faible devant l'accélération de la pesanteur permet d'assimiler un référentiel lié à la surface de la Terre à un référentiel galiléen.
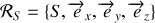 est supposé galiléen et les axes
est supposé galiléen et les axes
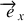 et
et
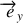 sont dans le plan de l'orbite terrestre supposée circulaire.
sont dans le plan de l'orbite terrestre supposée circulaire.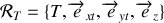 lié au centre de la terre qui est en rotation par rapport au référentiel
lié au centre de la terre qui est en rotation par rapport au référentiel
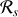 .
.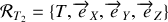 lié au centre de la terre qui est en rotation par rapport au référentiel
lié au centre de la terre qui est en rotation par rapport au référentiel
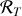 autour de l'axe
autour de l'axe
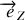 incliné de
incliné de
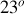 par rapport à l'axe
par rapport à l'axe
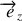 . La direction de l'axe de rotation
. La direction de l'axe de rotation
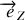 est fixe par rapport à
est fixe par rapport à
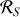 .
.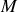 immobile situé à une lattitude
immobile situé à une lattitude
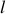 à la surface du Globe. Déterminer la vitesse et l'accélération de
à la surface du Globe. Déterminer la vitesse et l'accélération de
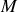 par rapport aux différents référentiels
par rapport aux différents référentiels
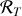 et
et
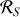 .
.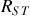 entre la Terre et le Soleil vaut environ
entre la Terre et le Soleil vaut environ
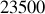 fois le rayon terrestre
fois le rayon terrestre
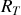 , donner une forme approchée de l'accélération de
, donner une forme approchée de l'accélération de
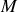 par rapport au référentiel
par rapport au référentiel
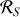 pour les points éloignés des pôles. On utilisera cette expression approchée pour la questions suivantes.
pour les points éloignés des pôles. On utilisera cette expression approchée pour la questions suivantes.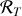 et
et
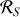 comme des référentiels galiléens.
comme des référentiels galiléens.