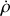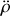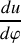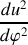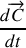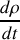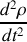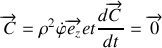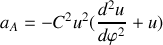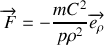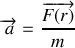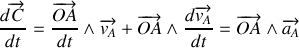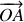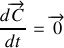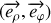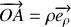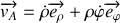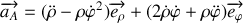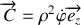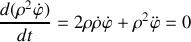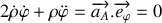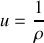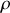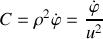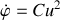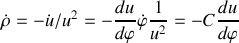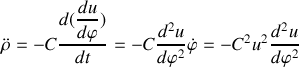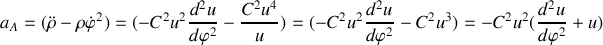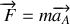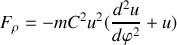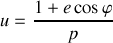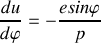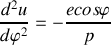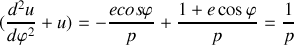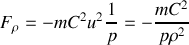Énoncé
Le mouvement d'un point
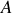 , de masse
, de masse
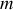 , dans le plan (
, dans le plan (
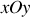 ) est défini par ses coordonnées polaires
) est défini par ses coordonnées polaires
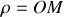 et
et
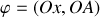 , où
, où
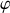 est l'angle entre l'axe
est l'angle entre l'axe
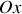 et la droite
et la droite
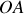 . On note
. On note
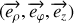 la base des coordonnées cylindriques. On désigne par
la base des coordonnées cylindriques. On désigne par
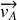 le vecteur vitesse du point
le vecteur vitesse du point
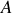 et par
et par
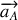 son vecteur accélération dans le référentiel 'fixe'
son vecteur accélération dans le référentiel 'fixe'
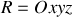 . On supposera que
. On supposera que
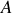 décrit une trajectoire dans le plan
décrit une trajectoire dans le plan
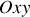 sous l'action d'une force centrale
sous l'action d'une force centrale
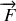 . Dans tout ce problème, les différents vecteurs seront calculés dans le référentiel
. Dans tout ce problème, les différents vecteurs seront calculés dans le référentiel
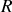 .
.
Donner la définition d'un mouvement à accélération centrale.
Montrer que le vecteur vitesse aréolaire
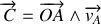 est un vecteur constant tout au long du mouvement de
est un vecteur constant tout au long du mouvement de
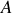 .
.Calculer l'expression générale du vecteur vitesse
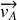 ainsi que celle du vecteur accélération
ainsi que celle du vecteur accélération
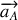 dans la base
dans la base
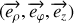 .
.En déduire l'expression du vecteur
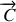 dans cette base ainsi qu'une relation reliant
dans cette base ainsi qu'une relation reliant
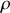 ,
,
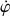 et le module de
et le module de
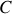 . Montrer que cette relation implique que la composante orthoradiale de l'accélération est nulle.
. Montrer que cette relation implique que la composante orthoradiale de l'accélération est nulle.On pose
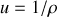 . On admet désormais que u est une fonction de
. On admet désormais que u est une fonction de
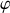 . Calculer l'expression du vecteur accélération
. Calculer l'expression du vecteur accélération
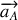 en fonction de
en fonction de
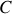 ,
,
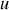 et
et
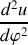
En utilisant la formule de Binet obtenue en question 5., trouver l'expression de la force qui s'exerce sur le point
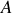 dans le cas où la trajectoire est une ellipse d'équation:
dans le cas où la trajectoire est une ellipse d'équation:
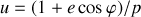 où
où
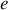 est l'excentricité et
est l'excentricité et
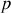 le paramètre de l'ellipse sont constants.
le paramètre de l'ellipse sont constants.Application à la répulsion coulombienne (c'est une hyperbole) entre 2 charges
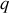 et
et
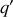 , une particule chargée positivement, dans le champ d'une autre particule fixe.
, une particule chargée positivement, dans le champ d'une autre particule fixe.