Énoncé
Un chariot de masse
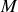 initialement immobile peut glisser sans frottement sur des rails horizontaux. Un tuyau, de section
initialement immobile peut glisser sans frottement sur des rails horizontaux. Un tuyau, de section
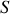 et d'axe parallèle aux rails, remplit le chariot de sable avec un débit massique
et d'axe parallèle aux rails, remplit le chariot de sable avec un débit massique
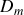 . Le sable tombe dans le chariot avec une vitesse constante, dans une direction faisant un angle
. Le sable tombe dans le chariot avec une vitesse constante, dans une direction faisant un angle
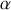 par rapport à l'horizontale et de module
par rapport à l'horizontale et de module
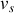 .
.
Déterminer la vitesse du chariot au cours du temps.
On rappelle que le débit massique est la quantité de matière traversant une section du tuyau par unité de temps. C'est aussi ici la masse de sable arrivant dans le chariot par unité de temps.
Pour obtenir l'équation différentielle gouvernant l'évolution temporelle de la vitesse du chariot, il faut appliquer la conservation de l'impulsion entre deux instants infiniment proches
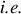 entre l'instant
entre l'instant
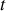 et l'instant
et l'instant
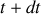 .
.
Le sable sortant du tuyau percute la surface de sable du chariot. Ces collisions "permanentes" transfèrent de l'impulsion du sable, en chute libre, au chariot. Pour obtenir l'équation différentielle gouvernant l'évolution temporelle de la vitesse du chariot, il faut appliquer la conservation de l'impulsion entre deux instants infiniment proches i.e. entre l'instant
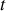 et l'instant
et l'instant
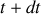 .
.
On pose
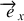 un vecteur unitaire aligné avec l'axe du tuyau et
un vecteur unitaire aligné avec l'axe du tuyau et
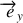 un vecteur unitaire vertical ascendant.
un vecteur unitaire vertical ascendant.
Bilan d'impulsion à l'instant
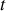 :
:
On prend en compte le chariot et le sable qui va tomber dans le chariot dans l'intervalle de temps
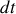 .
.
Le chariot vide a une masse
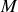 et il contient une masse
et il contient une masse
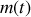 de sable ; il se déplace à une vitesse
de sable ; il se déplace à une vitesse
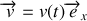 . L'impulsion du chariot à l'instant
. L'impulsion du chariot à l'instant
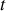 est donc
est donc
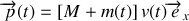 .
.
Pendant le "petit'' intervalle de temps
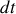 va tomber dans le chariot une "petite'' masse de sable
va tomber dans le chariot une "petite'' masse de sable
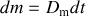 . L'intervalle de temps est choisi suffisamment petit pour que l'on puisse supposer que les grains de sable de
. L'intervalle de temps est choisi suffisamment petit pour que l'on puisse supposer que les grains de sable de
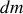 aient tous la même vitesse ; mais l'intervalle
aient tous la même vitesse ; mais l'intervalle
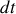 doit aussi être suffisamment grand pour qu'il y ait un certain nombre de grains de sable tombant dans le chariot, nécessaire à l'utilisation de notion de milieu continu comme le débit massique. C'est pourquoi l'intervalle de temps
doit aussi être suffisamment grand pour qu'il y ait un certain nombre de grains de sable tombant dans le chariot, nécessaire à l'utilisation de notion de milieu continu comme le débit massique. C'est pourquoi l'intervalle de temps
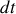 n'est pas infiniment petit mais juste petit.
n'est pas infiniment petit mais juste petit.
Dans ce cas, l'impulsion du sable qui va tomber dans le chariot est
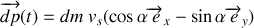 .
.
Bilan d'impulsion à l'instant
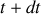 :
:
A l'instant
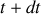 , le sable considéré précédemment est tombé dans le chariot qui a maintenant une masse
, le sable considéré précédemment est tombé dans le chariot qui a maintenant une masse
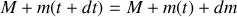 et une vitesse
et une vitesse
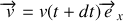 , soit une impulsion
, soit une impulsion
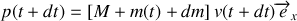
En l'absence de frottement, le chariot est soumis à deux forces
Son poids qui est vertical descendant,
La réaction des rails qui est verticale ascendante.
Les deux forces étant dans la direction
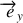 , il n'y a pas de force dans la direction
, il n'y a pas de force dans la direction
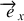 . Le sol étant assimilé à un référentiel galiléen, le principe fondamental de la dynamique nous permet d'affirmer qu'il y a conservation de la projection de l'impulsion dans la direction
. Le sol étant assimilé à un référentiel galiléen, le principe fondamental de la dynamique nous permet d'affirmer qu'il y a conservation de la projection de l'impulsion dans la direction
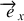 . On en déduit que
. On en déduit que
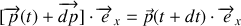
soit en utilisant les expressions obtenues dans le bilan d'impulsion :
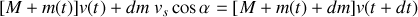
L'intervalle de temps
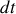 étant petit, on peut approcher
étant petit, on peut approcher
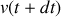 par son développement de Taylor tronqué au premier ordre
par son développement de Taylor tronqué au premier ordre
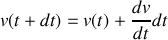 , ce qui revient à assumer une variation linéaire de la vitesse dans l'intervalle de temps
, ce qui revient à assumer une variation linéaire de la vitesse dans l'intervalle de temps
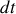 .
.
En reportant on obtient,
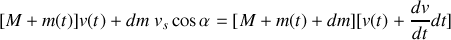
et après simplification
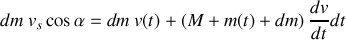
enfin, en remplaçant
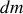 par son expression en fonction de
par son expression en fonction de
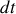
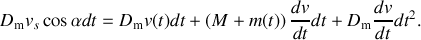
L'intervalle de temps
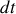 étant petit, le terme en
étant petit, le terme en
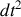 est négligeable devant les termes en
est négligeable devant les termes en
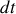 et on trouve finalement pour l'équation différentielle régissant l'évolution temporelle de la vitesse :
et on trouve finalement pour l'équation différentielle régissant l'évolution temporelle de la vitesse :
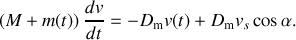
Résolution de l'équation différentielle :
Pour déterminer l'évolution de la vitesse du chariot, il faut au préalable déterminer l'évolution de la masse de sable dans le chariot, et ce pour remplacer
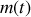 dans l'équation de la vitesse par une dépendance explicite en temps.
dans l'équation de la vitesse par une dépendance explicite en temps.
La variation de la masse est donnée par l'équation différentielle
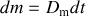 soit
soit
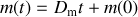 . En supposant qu'à l'instant initial le chariot est vide
. En supposant qu'à l'instant initial le chariot est vide
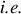
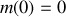 on obtient
on obtient
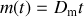 , d'où l'équation pour la vitesse du chariot :
, d'où l'équation pour la vitesse du chariot :
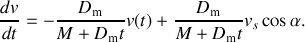
C'est une équation différentielle linéaire du premier ordre dont la solution est la somme d'une solution particulière et de la solution de l'équation homogène associée. La solution particulière
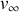 , qui représente la solution asymptotique, est ici une constante
, qui représente la solution asymptotique, est ici une constante
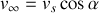 . La solution homogène est la solution de l'équation
. La solution homogène est la solution de l'équation
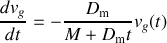
dont on peut séparer les variables pour les mettre sous la forme
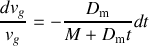
exprimant ainsi l'égalité en tous points des dérivées de deux fonctions. On en déduit l'égalité à une constante près de leurs primitives soit
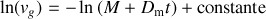
ou encore
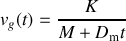
finalement, la solution générale
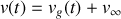 donnant l'évolution temporelle de la vitesse est
donnant l'évolution temporelle de la vitesse est
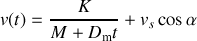
La vitesse du chariot étant nulle à l'instant initial, on a
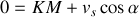 ce qui détermine la constante
ce qui détermine la constante
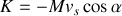 et ainsi l'évolution de la vitesse
et ainsi l'évolution de la vitesse
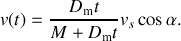
On retrouve effectivement que
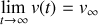 . Lorsque le module de la vitesse du chariot atteint la même valeur que la composante horizontale de la vitesse du sable, il n'y a plus de transfert d'impulsion horizontale.
. Lorsque le module de la vitesse du chariot atteint la même valeur que la composante horizontale de la vitesse du sable, il n'y a plus de transfert d'impulsion horizontale.



