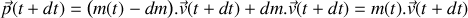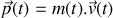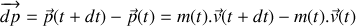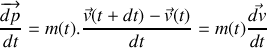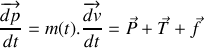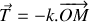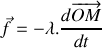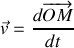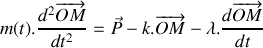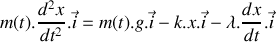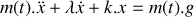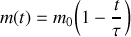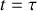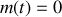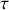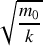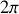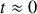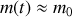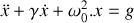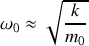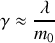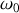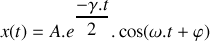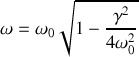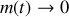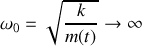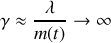On considère un bloc de masse 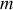constante attaché à un support horizontal fixe par l'intermédiaire d'un ressort de constante de raideur 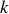et de masse négligeable.

Si on suppose que le bloc est soumis à une force de frottement de nature visqueuse de norme proportionnelle à la vitesse du bloc et de sens opposé à celle-ci ( 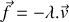, 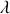est le coefficient de frottement), l'équation différentielle régissant l'évolution de la position 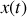du bloc s'écrit 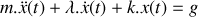où 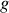représente l'accélération de la pesanteur.

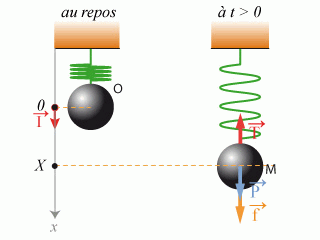
Pour dériver cette équation, l'origine des positions est le point 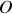repérant l'extrémité du ressort lorsque celui-ci n'est pas chargé ( ).

Figure 1 : schéma du dispositif.

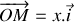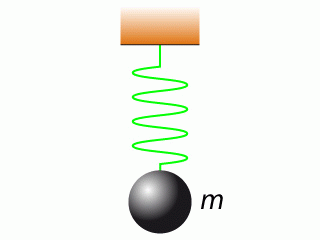
Le but de cet exercice est l'étude du comportement d'un tel système lorsque la masse suspendue n'est plus constante mais devient fonction du temps : 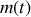. Pour réaliser ceci, il suffit par exemple d'attacher au ressort un récipient troué contenant du sable. Le sable s'écoule par l'orifice de sortie de sorte que la masse suspendue est une fonction décroissante du temps.

Les questions 1. et 2. sont indépendantes.

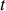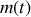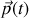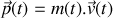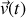1. A l'instant , la masse du récipient contenant le sable vaut de sorte que sa quantité de mouvement s'écrit où représente la vitesse du récipient de sable à l'instant 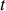. A l'instant 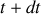, le récipient s'est vidé d'une quantité 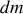de sable qui a été libérée du récipient avec une vitesse 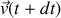égale à celle du bloc.

   1.a) Donner, à 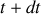, la quantité de mouvement 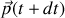de l'ensemble constitué de la masse de sable libérée et du récipient. En déduire l'accroissement 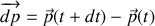de cette quantité de mouvement entre 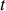et .

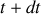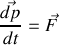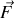   1.b) En utilisant la deuxième loi de Newton : , où représente la résultante des forces agissant sur le récipient, montrer que l'équation différentielle régissant l'évolution de la position du bloc s'écrit : .

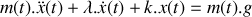   On supposera que le bloc est soumis à une force de frottement de nature visqueuse comme énoncé ci-dessus.

2. On suppose que la masse est une fonction linéairement décroissante du temps de sorte que 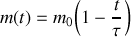avec 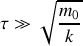. Dans cette question, on ne demande pas de résoudre des équations mais d'étayer les réponses sur la base d'arguments physiques simples.

   a) Quelle est la signification physique de l'hypothèse ?

   b) Quelle est la nature du mouvement du bloc si 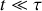? Préciser en particulier sa période et éventuellement la valeur du taux d'amortissement .

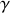   c) Quelle est la nature du mouvement du bloc si 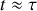? Préciser en particulier sa période et éventuellement la valeur du taux d'amortissement .

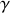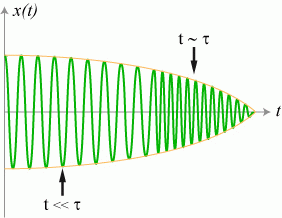
   d) Représenter schématiquement l'évolution de la position 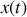du bloc dans le temps. On supposera que le bloc a été lâché sans vitesse initiale d'une position 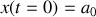. Attention, aucun calcul n'est demandé ; seuls les résultats obtenus aux questions 2.b et 2.c sont à utiliser pour répondre à cette question.