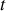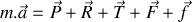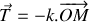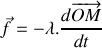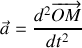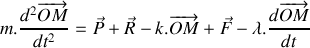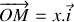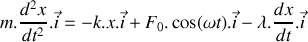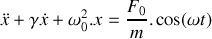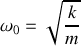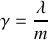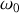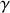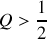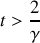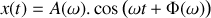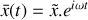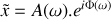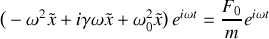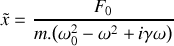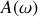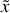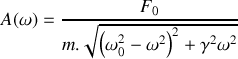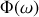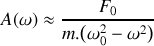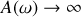Énoncé
On considère un bloc solide de masse
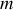 attaché par un ressort de constante de raideur
attaché par un ressort de constante de raideur
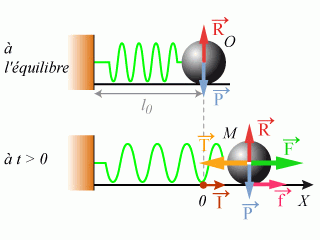
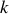 fixé à un support vertical. L'ensemble repose sur un support horizontal. A l'équilibre, le ressort n'est pas comprimé de sorte que sa longueur est égale à sa longueur à vide.
fixé à un support vertical. L'ensemble repose sur un support horizontal. A l'équilibre, le ressort n'est pas comprimé de sorte que sa longueur est égale à sa longueur à vide.
A l'instant
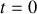 , on met en marche un système mécanique permettant de moduler de manière sinusoïdale la position du bloc tel que la force appliquée sur celui-ci s'écrit :
, on met en marche un système mécanique permettant de moduler de manière sinusoïdale la position du bloc tel que la force appliquée sur celui-ci s'écrit :
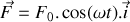 où
où
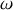 est la pulsation du forçage (ou de la modulation).
est la pulsation du forçage (ou de la modulation).
On suppose que le bloc est soumis à une force de frottement de type fluide de norme proportionnelle à sa vitesse et de sens opposé à celle-ci (
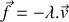 ,
,
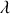 est le coefficient de frottement). On notera g l'accélération de la pesanteur. La loi de Hooke est supposée vérifiée dans tout l'exercice.
est le coefficient de frottement). On notera g l'accélération de la pesanteur. La loi de Hooke est supposée vérifiée dans tout l'exercice.
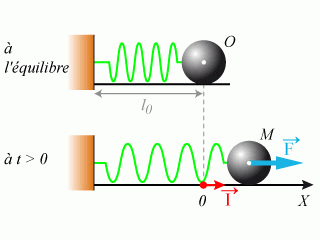
Etablir l'équation différentielle gouvernant l'évolution de la position
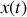 du bloc se déplaçant le long de l'axe
du bloc se déplaçant le long de l'axe
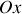 .
. On suppose que l'oscillateur étudié est tel que la solution de l'équation précédemment établie s'écrit :
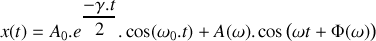 .
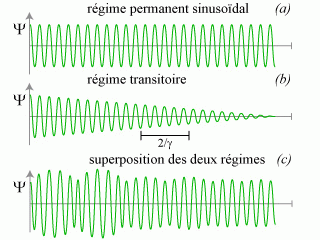
. Expliquer clairement à quel type de réponse de l'oscillateur correspond chacun des deux termes composant la fonction
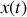 . Que pensez-vous du facteur de qualité de l'oscillateur étudié ? Est-il possible de négliger l'un des deux termes et si oui, expliquer à quelle(s) condition(s) ?
. Que pensez-vous du facteur de qualité de l'oscillateur étudié ? Est-il possible de négliger l'un des deux termes et si oui, expliquer à quelle(s) condition(s) ? Rappeler ce qu'est la notation complexe et l'utiliser pour déterminer
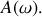
On considère que les frottements sont négligeables de sorte que
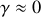 . Que devient l'amplitude des oscillations du bloc lorsque
. Que devient l'amplitude des oscillations du bloc lorsque
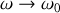 ? Nommer le phénomène physique auquel se rattache le comportement obtenu.
? Nommer le phénomène physique auquel se rattache le comportement obtenu.