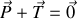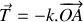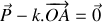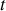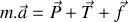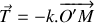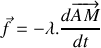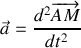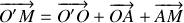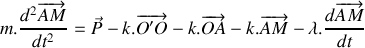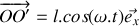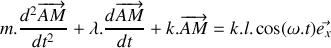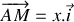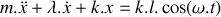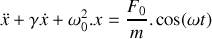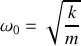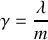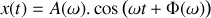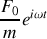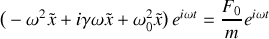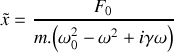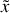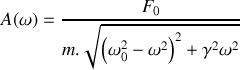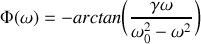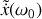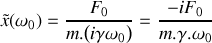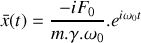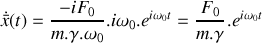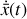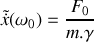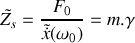L'alimentation en électricité des locomotives est assurée par un système appelé pantographe. Ce dispositif, solidaire de la locomotive, assure le captage du courant électrique en maintenant un contact électrique constant entre le fil d'alimentation et la locomotive. Les fils d'alimentation sont suspendus à des poteaux (régulièrement espacés le long de la voie) par l'intermédiaire de caténaires. Même si l'onde transverse générée par le pantographe le long du câble se déplace généralement plus rapidement que le train, elle peut être partiellement réfléchie au niveau des points de suspension, revenir vers le train et ainsi déconnecter le câble électrique du pantographe. Les caténaires sont donc des éléments essentiels à la bonne circulation des trains.

Schéma équivalent du dispositif

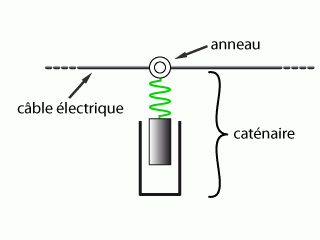
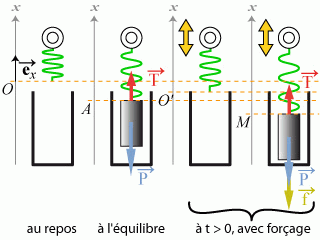
Dans ce modèle simple, le système de suspension du câble électrique est assimilé à un anneau connecté, par l'intermédiaire d'un ressort, à un piston coulissant dans un cylindre (voir ci-dessus).

La masse de l'anneau est négligeable. Celui-ci est attaché au piston de masse 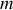par l'intermédiaire d'un ressort de constante de raideur 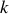(l'amplitude de déplacement du piston est toujours suffisamment faible pour que la loi de Hooke soit vérifiée).

Le piston coulisse selon la direction verticale dans un cylindre exerçant une force de frottement de type fluide de norme proportionnelle au vecteur vitesse et de sens opposé à celui-ci ( 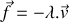, 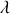est le coefficient de frottement).

Sous l'action du câble, l'anneau est soumis à un mouvement sinusoïdal selon la direction verticale (c'est-à-dire la direction 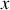de vecteur unitaire 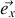) de sorte que 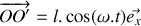(voir figure ci-dessous). 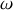représente la pulsation du forçage sinusoïdal et 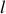est l'amplitude du mouvement de l'anneau. On notera 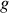l'accélération de la pesanteur.

Schéma du dispositif avec bilan des forces dans un référentiel galiléen

1. En prenant le point 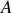comme origine du repère (voir figure ci-dessus), établir l'équation différentielle vectorielle gouvernant l'évolution de la position du piston .

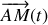   Montrer que l'équation différentielle gouvernant l'évolution de la position 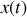du piston s'écrit : .

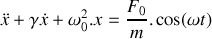   On exprimera les paramètres 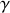, 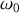et 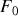en fonction de 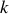, , 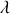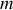et .

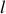2. On suppose désormais que le régime permanent sinusoïdal est établi de sorte que : .

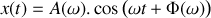   On rappelle que la représentation complexe de 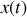s'écrit 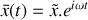avec 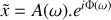. Déterminer l'expression de l'amplitude complexe 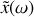du mouvement du piston.

3. On se place dans le cas où la pulsation du forçage est identique à la pulsation propre du système oscillant : .

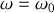   On définit l'impédance complexe 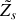de l'oscillateur comme le rapport entre 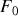et la représentation complexe de la vitesse  : .

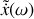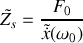   Déterminer l'expression analytique de 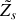en fonction 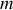de et de .

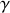   L'impédance complexe 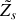est-elle réelle ou imaginaire pure? Que cela signifie t-il?