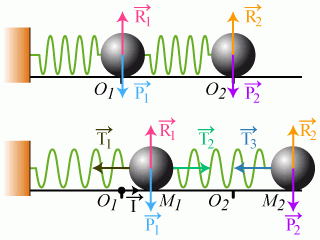
En appliquant le principe fondamental de la dynamique à t quelconque, il vient :
- Pour m_1 : m_1 . \vec{a_1} = \vec{P_1} + \vec{R_1} + \vec{T_1} + \vec {T_2}.
- Pour m_2 : m_2 . \vec{a_2} = \vec{P_2} + \vec{R_2} + \vec{T_3}.
La loi de Hooke donne : \left\{ \begin{array}{lc} \vec{T_1} = - k_1 . \overrightarrow{O_1 M_1} \\ \vec{T_2} = k_2 . ( \overrightarrow{M_1 M_2} - \overrightarrow{O_1 O_2} ) \\ \vec{T_3} = - k_2 . ( \overrightarrow{M_1 M_2} - \overrightarrow{O_1 O_2} )\end{array} \right.
Afin d'obtenir l'équation du mouvement dans les repères d'origine O_1 et O_2, il faut exprimer \; \vec {T_1}, \vecT_2 et \vec {T_3} en fonction de \overrightarrow{O_1 M_1} et/ou \overrightarrow{O_2 M_2} :
\left\{ \begin{array}{lc} \vec{T_2} = k_2 . ( \overrightarrow{M_1 M_2} - \overrightarrow{O_1 O_2} ) = k_2 . [( \overrightarrow{M_1 O_1} + \overrightarrow{O_1 O_2} + \overrightarrow{O_2 M_2} ) - \overrightarrow{O_1 O_2} ] = k_2 . ( \overrightarrow{O_2 M_2} - \overrightarrow{O_1 M_1} ) \\ \vec{T_3} = - k_2 . ( \overrightarrow{M_1 M_2} - \overrightarrow{O_1 O_2} ) = - k_2 . [( \overrightarrow{M_1 O_1} + \overrightarrow{O_1 O_2} + \overrightarrow{O_2 M_2} ) - \overrightarrow{O_1 O_2} ] = - k_2 . ( \overrightarrow{O_2 M_2} - \overrightarrow{O_1 M_1} ) \end{array} \right.
Avec \vec{a_1} = \frac {d^2 \overrightarrow{O_1 M_1 }} {dt^2}~ et ~\vec{a_2} = \frac {d^2 \overrightarrow{O_2 M_2 }} {dt^2} :
- Pour m_1 : m_1 . \frac {d^2 \overrightarrow{O_1 M_1 }} {dt^2} = \vec{P_1} + \vec{R_1} - (k_1 + k_2). \overrightarrow{O_1 M_1} + k_2 . \overrightarrow{O_2 M_2}.
- Pour m_2 : m_2 . \frac {d^2 \overrightarrow{O_2 M_2 }} {dt^2} = \vec{P_2} + \vec{R_2} + k_2 . \overrightarrow{O_1 M_1} - k_2 . \overrightarrow{O_2 M_2}.
\overrightarrow{O_1 M_1 } = x_1.\vec i, \overrightarrow{O_2 M_2 } = x_2.\vec i et après projection sur l'axe horizontal Ox, on obtient :
\left\{ \begin{array}{lc} m_1 . \ddot{x_1} = - (k_1 + k_2) . x_1 + k_2 . x_2 \\ m_2 . \ddot{x_2} = k_2 . x_1 - k_2 . x_2 }\end{array} \right
2.a) On a : m_1 = m_2 = m, k_1 = k, k_2 = \alpha k et \alpha \gg 1.
En divisant par m les équations obtenues à la question 1, on obtient :
\left\{ \begin{array}{lc} \ddot{x_1} = - \omega_0^2(1+\alpha). x_1 + \alpha.\omega_0^2 . x_2 \\ \ddot{x_2} = \alpha.\omega_0^2 . x_1 - \alpha.\omega_0^2 . x_2 }\end{array} ~~~~ avec \omega_0 = \root{}{\frac k m}
Sous forme vectorielle, ce système s'écrit :
\frac{d^2 \vec{X}} {dt^2 } = A . \vec{X}~, avec : ~~A = \omega_0^2.\left( \begin{array}{cc} - 1- \alpha && \alpha \\ \alpha && - \alpha \end{array} \right)~
et ~~\vecX = \left( \begin{array}{cc} x_1(t) \\ x_2(t) \end{array} \right).
Finalement, avec \pm1\pm\alpha~\approx~\pm\alpha~ : ~~A \approx \omega_0^2.\left( \begin{array}{cc} - \alpha && \alpha \\ \alpha && - \alpha \end{array} \right)~
On cherche alors une solution réelle de la forme \vecX = \vecX_0 . e^{\omega t}
En dérivant deux fois cette solution par rapport au temps et en remplaçant dans l'équation vectorielle, il vient :
\omega^2 . \vec {X_0} . e^{\omega t} = A . \vec {X_0} . e^{\omega t} \; \to \; \; \omega^2 . \vec {X_0} = A . \vec {X_0}
En posant \lambda = \omega^2, on a alors un problème aux valeurs propres A . \vec {X_0} = \lambda . \vec {X_0} avec \lambda valeur propre de A et \vec {X_0} vecteur propre de A.
Pour déterminer les valeurs propres, il faut résoudre : det (A - \lambda . Id ) = 0.
\left| \begin{array}{cc} - \alpha.\omega_0^2 - \lambda && \alpha.\omega_0^2 \\ \alpha.\omega_0^2 && - \alpha.\omega_0^2 - \lambda \end{array} \right|=0.
D'où : ( \alpha.\omega_0^2 + \lambda )^2 - \alpha^2.\omega_0^4= 0 \; \to \; \; \lambda^2 + 2.\lambda . \alpha.\omega_0^2 = 0 \; \to \; \; \lambda . (\lambda + 2 . \alpha. \omega_0^2 ) = 0
On a alors une équation du second degré avec deux solutions possibles : \left\{ \begin{array}{l} \lambda_1=0 \\ \lambda_2 = - 2.\alpha.\omega_0^2 \end{array}~~
. Ce sont les valeurs propres de A.
Pour déterminer les vecteurs propres, il faut résoudre : A . \vec {X_1} = \lambda_1 . \vec {X_1} et A . \vec {X_2} = \lambda_2 . \vec {X_2} .
Ici : \omega_0^2.\left( \begin{array}{cc} - \alpha && \alpha \\ \alpha && - \alpha \end{array} \right)~.~\left( \begin{array}{cc} X_1 \\ Y_1 \end{array} \right) = \vec0 \; \to \; \; X_1 = Y_1
On choisit en général l'unité pour la valeur de X_1, soit : \vec {X_1} = \left( \begin{array}{cc} 1 \\ 1 \end{array} \right)
De la même façon :
\omega_0^2.\left( \begin{array}{cc} - \alpha && \alpha \\ \alpha && - \alpha \end{array} \right)~.~\left( \begin{array}{cc} X_2 \\ Y_2 \end{array} \right) = - 2.\alpha.\omega_0^2~.~\left( \begin{array}{cc} 1 && 0 \\ 0 && 1 \end{array} \right)~.~\left( \begin{array}{cc} X_2 \\ Y_2 \end{array} \right)\; \to \; \;\left( \begin{array}{cc} -\alpha.\omega_0^2. X_2+\alpha.\omega_0^2.Y_2 = - 2.\alpha.\omega_0^2.X_2 \\ \alpha.\omega_0^2. X_2- \alpha.\omega_0^2.Y_2 = - 2.\alpha.\omega_0^2.X_2 \end{array} \right) \; \to \; \; X_2 = - Y_2
Soit : \vec {X_2} = \left( \begin{array}{cc} 1 \\ - 1 \end{array} \right)
On a alors :
- ~~\vec {X_1} = \left( \begin{array}{cc} 1 \\ 1 \end{array} \right) le vecteur propre associé à la valeur propre \lambda_1 = 0
- ~~\vec {X_2} = \left( \begin{array}{cc} 1 \\ - 1 \end{array} \right) le vecteur propre associé à la valeur propre \lambda_2 = - 2.\alpha.\omega_0^2
2.b) La solution générale du système d'équations est de la forme \vecX = \vecX_0 . e^{\omega t}. Avec \lambda = \omega^2, il s'agit d'une combinaison linéaire des solutions aux valeurs propres telle que :
\vecX = a. e^{i\root {}{|\lambda_1|}}.\vecX_1 + b. e^{- i\root {}{|\lambda_1|}}.\vecX_1 + c. e^{i\root {}{|\lambda_2|}}.\vecX_2 + d. e^{-i\root {}{|\lambda_2|}}.\vecX_2~ où a, b, c et d sont des constantes.
Ici :\vecX = \left( \begin{array}{cc} x_1(t) \\ x_2(t) \end{array} \right) = a.\left( \begin{array}{cc} 1 \\ 1 \end{array} \right) + c. e^{i\omega_0\root{}{2\alpha}.t}.\left( \begin{array}{cc} 1 \\ - 1 \end{array} \right) + d. e^{-i\omega_0\root{}{2\alpha}.t}.\left( \begin{array}{cc} 1 \\ - 1 \end{array} \right)
D'où : \left\{ \begin{array}{lc} x_1(t) = a + A_1.\cos(\omega_0\root{}{2\alpha}.t + \varphi_1) \\ x_2(t) = a - A_1.\cos(\omega_0\root{}{2\alpha}.t + \varphi_1) \end{array} \right.
où A_1 et \varphi_1 sont les constantes d'intégration.
2.c) Le mouvement peut être décomposé en une superposition (somme) de mouvements harmoniques appelés modes propres (ou modes normaux) de vibration.
On reconnaît ici la solution d'un oscillateur harmonique du type q(t) = A.\cos(\omega.t + \varphi). Dans le cas présent, il n'y a qu'une seule solution de cette forme dans x_1 (t) et x_2 (t).
Le seul mode propre du système est alors :
q_1(t) = A_1.\cos(\omega_0\root{}{2\alpha}.t + \varphi_1) avec \omega_0\root{}{2\alpha} sa pulsation propre.
N.B. : ce résultat est cohérent avec le fait que le système ne possède qu'une valeur propre non nulle \lambda_2.
On peut déterminer les constantes d'intégration A_1 et \varphi_1 à partir des conditions initiales :
\left\{ \begin{array}{lc} x_1 (t = 0) = a_0 = a + A_1.\cos(\varphi_1) && (1) \\ \dot{x_1}(t = 0) = 0 = - A_1.\omega_0\root{}{2\alpha}.\sin(\varphi_1) && (2) \end{array}\right
et ~\left\{ \begin{array}{lc} x_2 (t = 0) = - a_0 = a - A_1.\cos(\varphi_1) && (3) \\ \dot{x_2}(t = 0) = 0 = A_1.\omega_0\root{}{2\alpha}.\sin(\varphi_1) && (4) \end{array}\right
A_1, \omega_0 et \alpha étant forcément non nulles, les équations (2) et (4) donnent ~~\sin (\varphi_1) = 0 \; \to \; \;\varphi_1 = 0.
Avec \varphi_1 = 0 \; \to \; \; \cos(\varphi_1) = 1, les équations (1) et (3) donnent :
~\left\{ \begin{array}{lc} a + A_1 = a_0 \\ a - A_1 = - a_0 \end{array} \; \to \; \; \left\{ \begin{array}{lc} a = 0 \\ A_1 = a_0 \end{array}.
Finalement : \left\{ \begin{array}{lc} x_1 = a_0 . \cos (\omega_0 \root{}{2 \alpha} . t) \\ x_2 = - a_0 . \cos (\omega_0 \root{}{2 \alpha} . t) = a_0 . \cos (\omega_0 \root{}{2 \alpha} . t + \pi) \end{array}
Lorsque q_1(t) est excité par ces conditions initiales, les deux masses se déplacent avec la même amplitude en opposition de phase.