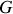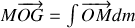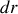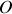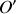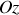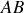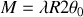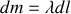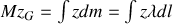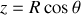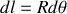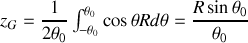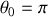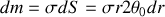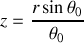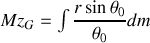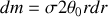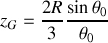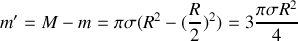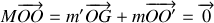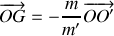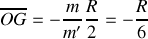L'axe de symétrie
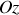 de l'arc
de l'arc
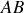 supposé homogène contient le centre d'inertie
supposé homogène contient le centre d'inertie
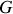 .
.
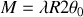 La position du centre d'inertie
La position du centre d'inertie
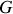 est telle que :
est telle que :
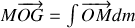 avec
avec
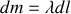 Projetons sur l'axe
Projetons sur l'axe
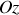 :
:
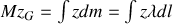
avec
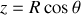 et
et
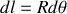
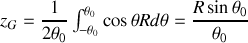
Pour un cercle entier (
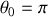 ), on vérifie que
), on vérifie que
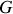 est en
est en
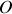 .
.
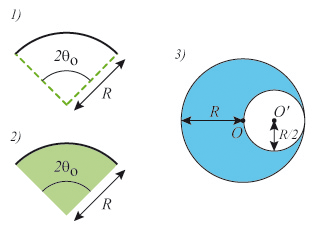
De même que précédemment, l'axe de symétrie
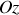 de l'arc
de l'arc
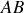 supposé homogène contient le centre d'inertie
supposé homogène contient le centre d'inertie
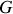 .
.
Soit un arc d'épaisseur
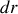 et de masse
et de masse
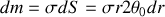 Le centre d'inertie d'un tel arc est d'après la question précédente en
Le centre d'inertie d'un tel arc est d'après la question précédente en
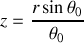 . Le centre d'inertie de l'ensemble est tel que :
. Le centre d'inertie de l'ensemble est tel que :
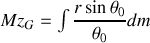
avec
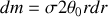
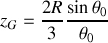 .
.
Soient
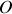 et
et
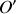 les centres d'inertie du disque complet et du disque enlevé et
les centres d'inertie du disque complet et du disque enlevé et
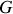 celui du disque perforé. Le disque perforé a une masse
celui du disque perforé. Le disque perforé a une masse
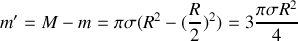 . Le disque entier peut être vu comme l'association du disque perforé et du disque de rayon
. Le disque entier peut être vu comme l'association du disque perforé et du disque de rayon
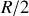 .
.
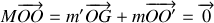 donc
donc
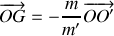
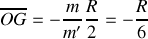 . Comme on pouvait s'y attendre, le centre d'inertie
. Comme on pouvait s'y attendre, le centre d'inertie
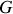 se trouve à gauche de
se trouve à gauche de
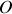 .
.
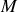 et d'angle d'ouverture
et d'angle d'ouverture
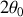
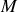 et d'angle d'ouverture
et d'angle d'ouverture
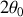
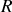 dans lequel on a découpé un disque de rayon
dans lequel on a découpé un disque de rayon
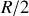 dont le centre est la distance
dont le centre est la distance
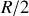 de celui du disque initial.
de celui du disque initial.