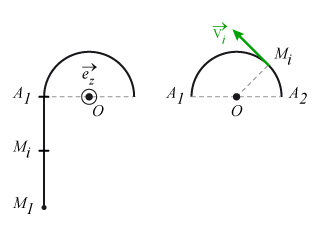
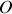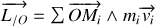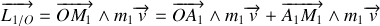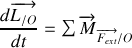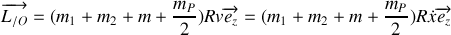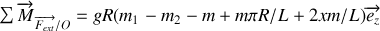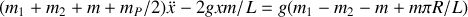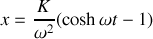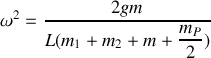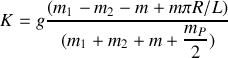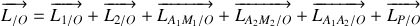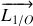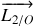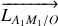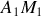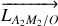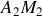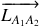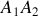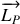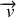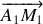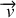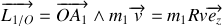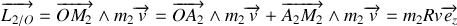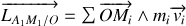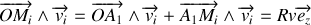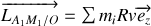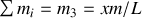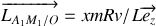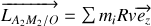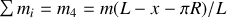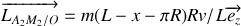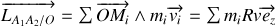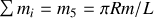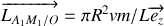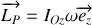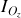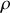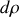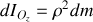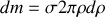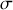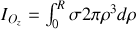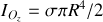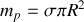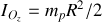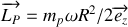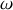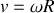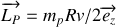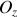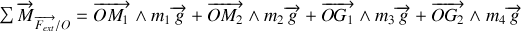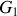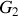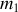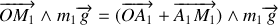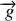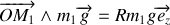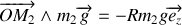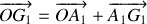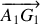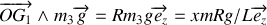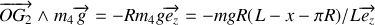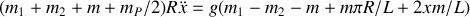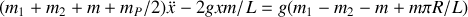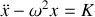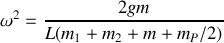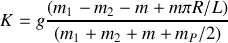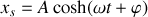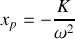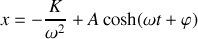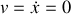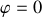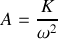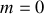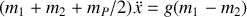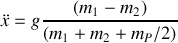Décomposons le moment cinétique :
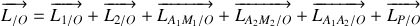
avec
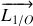 moment cinétique par rapport à
moment cinétique par rapport à
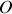 de la masse
de la masse
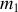
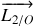 moment cinétique par rapport à
moment cinétique par rapport à
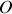 de la masse
de la masse
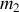
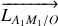 moment cinétique par rapport à
moment cinétique par rapport à
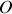 de la portion de fil
de la portion de fil
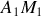
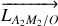 moment cinétique par rapport à
moment cinétique par rapport à
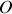 de la portion de fil
de la portion de fil
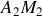
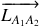 moment cinétique par rapport à
moment cinétique par rapport à
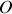 de la portion de fil
de la portion de fil
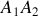 reposant sur la poulie
reposant sur la poulie
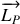 moment cinétique par rapport à
moment cinétique par rapport à
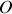 de la poulie
de la poulie
Soit
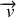 la vitesse de la masse
la vitesse de la masse
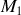 . Le fil étant inextensible, les 2 masses ont même vitesse.
. Le fil étant inextensible, les 2 masses ont même vitesse.
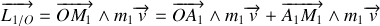
comme
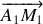 et
et
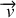 sont colinéaires, il reste:
sont colinéaires, il reste:
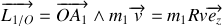
De même pour la masse
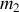 ,
,
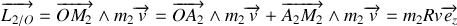
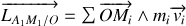 or
or
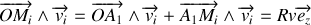 , tous les points du fil étant animés de la même vitesse.
, tous les points du fil étant animés de la même vitesse.
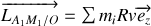
pour le segment
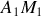 ,
,
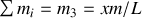
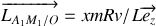
De même pour le segment
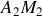 ,
,
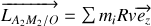
pour le segment
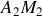 ,
,
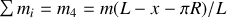
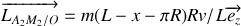
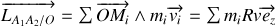
pour le segment
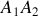 ,
,
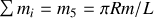
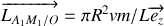
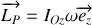
Il reste à calculer le moment d'inertie
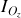 pour un disque homogène autour de son axe de rotation. Décomposons le disque en anneaux homogènes concentriques de rayon
pour un disque homogène autour de son axe de rotation. Décomposons le disque en anneaux homogènes concentriques de rayon
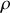 et d'épaisseur
et d'épaisseur
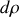 . Chacun de ces anneaux a un moment d'inertie
. Chacun de ces anneaux a un moment d'inertie
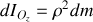
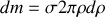 où
où
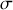 représente la densité surfacique. Pour le disque complet,
représente la densité surfacique. Pour le disque complet,
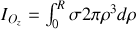
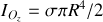 . La relation qui relie
. La relation qui relie
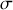 à
à
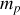 est la suivante:
est la suivante:
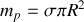
donc
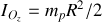
d'où
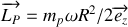
La poulie effectue un mouvement de rotation à la vitesse angulaire
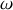 suite à la translation du fil avec la vitesse
suite à la translation du fil avec la vitesse
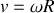
soit
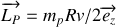
On en déduit le moment cinétique total:
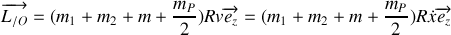 .
.
Bilan des forces extérieures agissant sur le système comprenant les 2 masses, le fil et la poulie :
Poids du fil, i.e. des parties
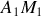 ,
,
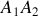 ,
,
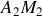
Poids de chacune des 2 masses
Poids de la poulie
Quelles sont les forces pour lesquelles le moment par rapport à
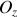 est égal au vecteur nul ?
est égal au vecteur nul ?
Poids de la poulie, la droite d'action intercepte l'axe de rotation
Poids de la portion de fil
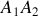 , idem
, idem
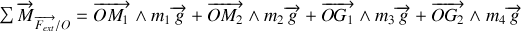
avec
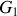 et
et
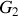 milieux des segments
milieux des segments
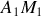 et
et
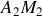 respectivement.
respectivement.
Pour le poids de la masse
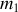 ,
,
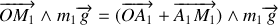
Comme
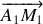 et
et
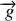 sont colinéaires,
sont colinéaires,
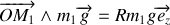
De la même façon pour la masse
 ,
,
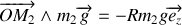 On peut décomposer
On peut décomposer
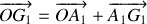
Comme
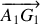 et
et
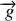 sont colinéaires,
sont colinéaires,
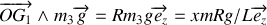
De la même façon,
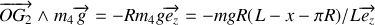
Donc
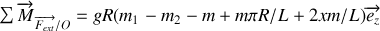 .
.
On écrit le théorème du moment cinétique:
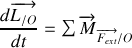 En remplaçant avec les résultats des questions précédentes,
En remplaçant avec les résultats des questions précédentes,
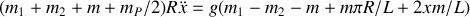
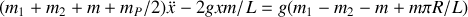
On obtient une équation différentielle de la forme :
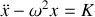
avec
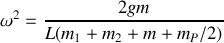
et
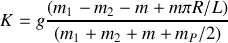
La solution sans second membre est de la forme
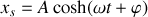
Une solution particulière s'écrit:
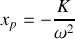
La solution générale avec second membre s'écrit:
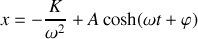
Or à
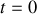 ,
,
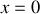 et
et
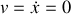
d'où
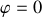 et
et
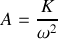
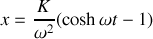
Cette équation est caractéristique d'un mouvement oscillant. Si on néglige la masse du fil,
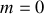 , l'équation différentielle se simplifie de la façon suivante :
, l'équation différentielle se simplifie de la façon suivante :
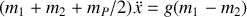
soit
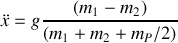
On retrouve l'équation différentielle d'un mouvement uniformément accéléré .
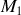 et
et
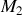 , de masses respectives
, de masses respectives
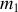 et
et
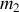 sont reliés par un fil inextensible de longueur
sont reliés par un fil inextensible de longueur
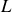 et de masse
et de masse
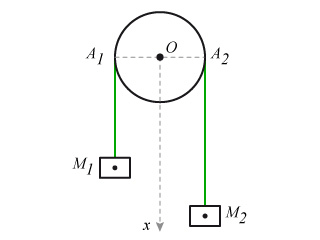
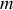 non négligeable, passant dans la gorge d'une poulie. Cette poulie sera considérée comme un disque homogène de masse
non négligeable, passant dans la gorge d'une poulie. Cette poulie sera considérée comme un disque homogène de masse
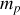 et de rayon
et de rayon
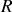 . La masse
. La masse
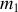 étant supérieure à la masse
étant supérieure à la masse
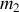 , le système débloqué à l'instant
, le système débloqué à l'instant
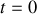 se met en mouvement.
se met en mouvement.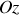 de la poulie.
de la poulie.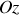 .
.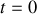
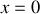 . Que deviennent ces résultats si la masse du fil est négligeable devant les masses en présence.
. Que deviennent ces résultats si la masse du fil est négligeable devant les masses en présence.