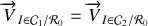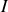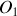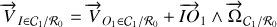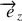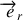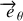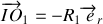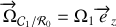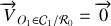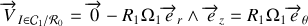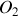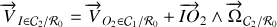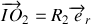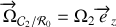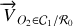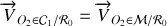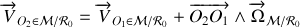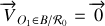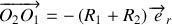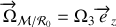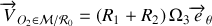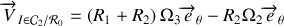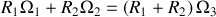Énoncé
Un cylindre
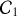de rayon
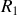, d'axe
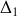horizontal, tourne avec une vitesse angulaire constante
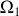. L'axe
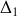est fixe par rapport à un référentiel galiléen noté
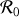. Un second cylindre
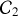de rayon
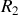et d'axe
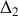horizontal, roule sur
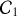en tournant autour de son axe avec une vitesse angulaire
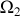. Les axes
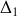et
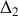sont reliés par une manivelle
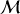de longueur
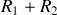qui les maintient à distance constante. La manivelle
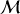tourne autour de
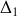avec une vitesse angulaire
.
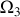Montrer que l'hypothèse du roulement sans glissement impose une contrainte sur les vitesses de rotation
,
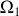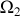et
.
