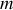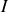Pour répondre a cette question, considérer une balle ou un cylindre de masse , de rayon et de moment d'inertie par rapport à l'axe de rotation. On note 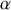l'angle d'inclinaison du plan avec l'horizontale.

1. En utilisant la conservation de l'énergie, déterminer l'équation différentielle donnant l'altitude en fonction du temps.

2. Déterminer ensuite le temps de trajet pour une dénivellation de hauteur de .

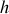3. Déterminer les moments d'inertie des différents solides.

4. En déduire l'ordre d'arrivée.

à compléter

NLP_C_M02_G01

à compléter

1. Pour répondre à cette question, considérons une balle ou un cylindre de masse 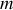, de rayon et de moment d'inertie 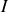par rapport à l'axe de rotation. On note 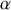l'angle d'inclinaison du plan avec l'horizontale.

   L'énergie mécanique est la somme de l'énergie cinétique de translation du centre de masse, de l'énergie cinétique de rotation et de l'énergie potentiel de pesanteur. En notant 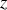, l'altitude de l'objet (l'axe 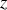est dirigé suivant la verticale ascendante), 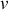la vitesse de translation du centre de masse et 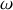la vitesse de rotation on obtient comme expression de l'énergie mécanique :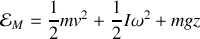

   

   Le roulement sans glissement impose une relation entre la vitesse de translation 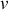et la vitesse de rotation : .

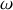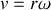   En remarquant qu'un déplacement élémentaire 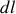le long du plan correspond une variation l'altitude 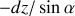on déduit la relation entre la vitesse 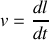et la vitesse de variation de l'altitude .

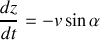   Enfin, en prenant l'origine de l'axe verticale 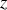au point de départ du mouvement, on obtient la valeur initiale de l'énergie mécanique .

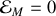   Finalement, en utilisant la conservation de l'énergie mécanique on obtient la relation suivante

   

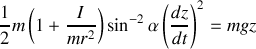
   Soit l'équation recherchée :

   

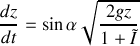
   où l'on a introduit la quantité .

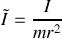2. L'équation différentielle se résout sans difficulté en séparant les variables

   

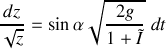
   et l'on obtient en tenant compte de la condition initiale

   

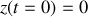
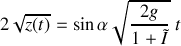
   soit pour le temps de parcours :

   

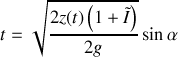
   Pour une dénivellation d'altitude de 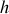, le temps de parcours est donc :

   .

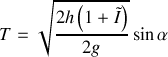   Minimiser ce temps de parcours revient donc à minimiser .

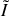3. Calculons maintenant la quantité 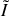pour les différents solides proposés.

   Pour le cylindre creux :

   

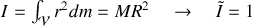
   Pour le cylindre plein :

   

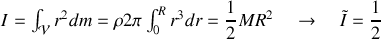
   Pour la boule, on note 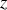l'axe de rotation. L'invariance de l'objet par rotation permet d'affirmer que 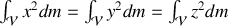soit

   

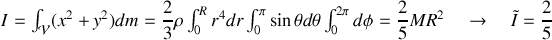
   Pour la balle creuse, on décompose le solide en une boule de rayon 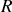et de masse 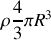  et une boule de rayon 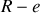et de masse 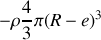  soit :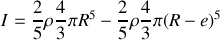

   

   en introduisant la masse 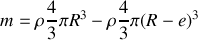et en faisant tendre 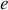vers

   

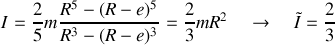
4. L'ordre d'arrivée est donc balle pleine, cylindre plein, balle creuse et cylindre creux.