Énoncé
Pour déterminer le moment d'inertie
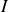 d'un corps par rapport à axe
d'un corps par rapport à axe
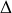 passant par le centre de gravité
passant par le centre de gravité
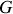 de ce corps, on le suspend en accrochant deux fils identiques de masses négligeables et de longueurs
de ce corps, on le suspend en accrochant deux fils identiques de masses négligeables et de longueurs
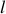 aux extrémités de l'axe
aux extrémités de l'axe
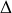 , maintenant ainsi l'axe
, maintenant ainsi l'axe
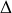 horizontal. Puis on mesure la durée d'une demi-oscillation dans la direction transverse à l'axe
horizontal. Puis on mesure la durée d'une demi-oscillation dans la direction transverse à l'axe
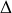 . En déduire le moment d'inertie
. En déduire le moment d'inertie
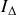 .
.
Utiliser la conservation de l'énergie mécanique pour obtenir une équation différentielle du premier ordre portant sur l'angle déviation du pendule.
Le pendule oscille dans le plan transverse à l'axe
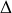 , les deux fils formant un angle identique
, les deux fils formant un angle identique
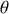 avec la verticale. Appelons
avec la verticale. Appelons
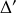 l'axe parallèle à
l'axe parallèle à
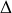 passant par les points d'attache des fils au plafond.
passant par les points d'attache des fils au plafond.
L'énergie cinétique du solide se compose de l'énergie cinétique de translation du centre de gravité et de l'énergie cinétique de rotation autour de l'axe passant par le centre de gravité :
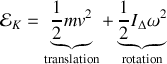
où
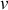 est la vitesse de translation du centre de gravité ici
est la vitesse de translation du centre de gravité ici
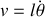 et
et
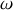 la vitesse de rotation autour de l'axe
la vitesse de rotation autour de l'axe
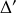 .
.
On détermine facilement les relations entre
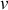 ,
,
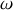 et l'angle
et l'angle
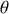 paramétrant la position du solide :
paramétrant la position du solide :
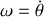 et
et
 .
.
En regroupant ces résultats, on trouve :
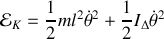
Remarquons que l'on aurait pu aussi décrire le mouvement comme une rotation autour de l'axe
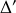 dans ce cas l'énergie cinétique aurait pris la forme
dans ce cas l'énergie cinétique aurait pris la forme
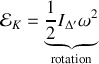
Le moment d'inertie par rapport à l'axe
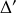 se déterminant en utilisant le théorème de Huygens :
se déterminant en utilisant le théorème de Huygens :
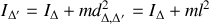 .
.
ce qui donne bien évidement le même résultat.
L'énergie potentiel est composée uniquement d'énergie potentiel de pesanteur :
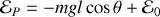
Soit pour l'énergie mécanique :
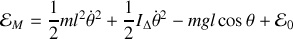 .
.
L'énergie mécanique est une constante du mouvement. Il est commode de l'évaluer au point de rebroussement du pendule c'est-à-dire à l'angle de déviation maximal
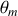 où la vitesse s'annule et où toute l'énergie mécanique est sous forme d'énergie potentiel.
où la vitesse s'annule et où toute l'énergie mécanique est sous forme d'énergie potentiel.
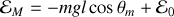 .
.
On en déduit l'équation différentielle portant sur l'angle
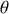 :
:
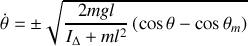
On obtient en fait deux équations différentielles, une pour les valeurs croissantes de
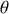 et l'autre pour les valeurs décroissantes. En appelant
et l'autre pour les valeurs décroissantes. En appelant
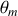 l'angle de déviation maximal du pendule, l'équation différentielle avec la racine positive décrit l'oscillation de
l'angle de déviation maximal du pendule, l'équation différentielle avec la racine positive décrit l'oscillation de
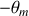 à
à
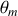 . Le temps
. Le temps
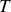 d'une demi-oscillation correspond à l'intégrale
d'une demi-oscillation correspond à l'intégrale
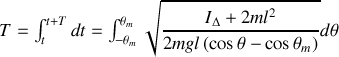
Cette intégrale se détermine simplement dans l'approximation des petits angles (
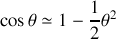 )
)
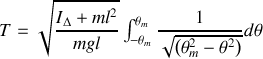
soit en posant
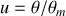 :
:
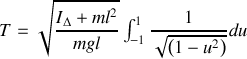 .
.
Or la primitive de la fonction
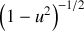 est la fonction
est la fonction
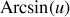 soit :
soit :
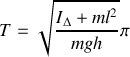 .
.
On en déduit la relation
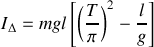
Lorsque le moment d'inertie est nul (cas d'un point matériel) on retrouve la relation
 qui correspond bien à la demi période d'un pendule simple.
qui correspond bien à la demi période d'un pendule simple.
On obtient ainsi une mesure simple du moment d'inertie. Pour que la mesure soit plus sensible, il est nécessaire de prendre une longueur de fil
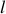 la plus courte possible. En effet si l'on appelle
la plus courte possible. En effet si l'on appelle
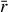 le rayon moyen de l'objet autour de l'axe
le rayon moyen de l'objet autour de l'axe
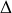 , alors
, alors
 et de l'ordre de
et de l'ordre de
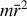 . Pour que l'influence du moment d'inertie soit significative il faut que
. Pour que l'influence du moment d'inertie soit significative il faut que
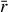 ne soit pas négligeable devant l.
ne soit pas négligeable devant l.



