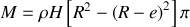Énoncé
Déterminer les axes principaux et les moments d'inertie des solides homogènes suivants
Un parallélépipède rectangle de coté
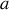 ,
,
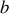 ,
,
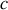 , étudier les cas
, étudier les cas
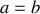 et
et
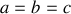 .
.Une boule de rayon
 .
.Une balle creuse de rayon
 et d'épaisseur
et d'épaisseur
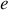 .
.Un cylindre de rayon
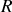 et de hauteur
et de hauteur
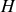 .
.Un tuyau de rayon extérieur
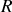 de hauteur
de hauteur
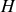 et d'épaisseur
et d'épaisseur
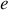 .
.
Utiliser la symétrie des objets pour déterminer les axes principaux.
Le parallélépipède étant homogène, le centre de gravité
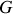 est à l'intersection des diagonales. Il possède trois plans de symétrie parallèles aux faces, on en déduit que les trois axes principaux sont les axes passant par les centres des faces opposées. En introduisant un repère cartésien
est à l'intersection des diagonales. Il possède trois plans de symétrie parallèles aux faces, on en déduit que les trois axes principaux sont les axes passant par les centres des faces opposées. En introduisant un repère cartésien
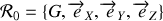 avec le vecteur
avec le vecteur
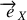 parallèle aux arrêtes de longueur
parallèle aux arrêtes de longueur
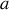 , le vecteur
, le vecteur
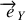
parallèle aux arrêtes de longueur
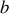 et le vecteur
et le vecteur
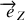 parallèle aux arrêtes de longueur
parallèle aux arrêtes de longueur
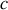 .
. 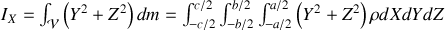
En décomposant les intégrales il vient :
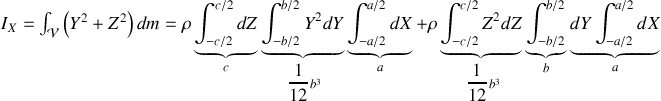
soit
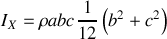
et finalement en introduisant la masse
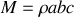 du solide
du solide 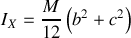
De la même façon, on obtient :
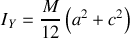
et
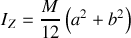
Le centre de gravité
 d'une boule homogène est au centre de la boule est comme tout axe passant par
d'une boule homogène est au centre de la boule est comme tout axe passant par
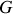 est un axe de symétrie d'ordre supérieur à
est un axe de symétrie d'ordre supérieur à
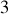 , tout axe passant par
, tout axe passant par
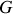 est un axe principal d'inertie. On introduit le repère cartésien
est un axe principal d'inertie. On introduit le repère cartésien
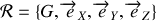 , les axes étant choisis sans distinction.
, les axes étant choisis sans distinction.Les trois axes principaux étant aussi des axes de symétrie d'ordre supérieur à trois, les trois moments d'inertie sont égaux:
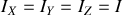 avec
avec 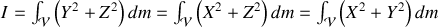
On en déduit facilement que
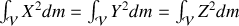
Au lieu de faire le calcul directement, il est plus simple de calculer
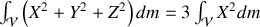
car l'intégrale
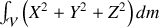 se calcul simplement en passant aux coordonnées polaires :
se calcul simplement en passant aux coordonnées polaires :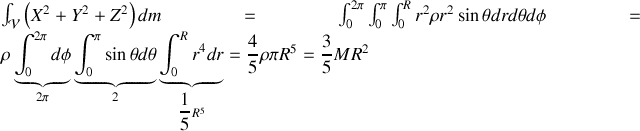
où l'on a introduit la masse
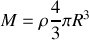 . Soit finalement
. Soit finalement 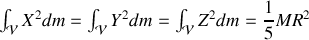 et donc
et donc
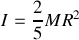
La balle creuse possède les mêmes symétries que la boule, on en déduit donc que le centre de gravité
 est au centre de la balle et que les trois axes du repère cartésien
est au centre de la balle et que les trois axes du repère cartésien
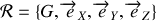 sont des axes principaux d'inertie de moments égaux
sont des axes principaux d'inertie de moments égaux
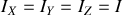 . Pour calculer le moment d'inertie, on peut décomposer la balle creuse en une boule homogène de rayon
. Pour calculer le moment d'inertie, on peut décomposer la balle creuse en une boule homogène de rayon
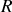 à laquelle on a prélevé une boule homogène de rayon
à laquelle on a prélevé une boule homogène de rayon
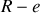 . Dès lors, on peut calculer
. Dès lors, on peut calculer
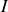 comme
comme 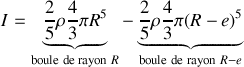
soit en introduisant la masse
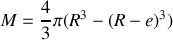
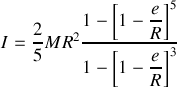
Le cylindre étant homogène, le centre de gravité
 est situé au milieu de l'axe de symétrie
est situé au milieu de l'axe de symétrie
 , l'axe
, l'axe
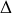 est donc un axe principal d'inertie. Tout plan contentant
est donc un axe principal d'inertie. Tout plan contentant
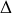 est un plan de symétrie donc les deux autres axes principaux sont perpendiculaires à
est un plan de symétrie donc les deux autres axes principaux sont perpendiculaires à
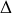 et passent par le centre de gravité. On introduit le repère cartésien
et passent par le centre de gravité. On introduit le repère cartésien
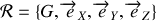 en alignant
en alignant
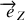 le long de l'axe
le long de l'axe
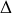 .
.Comme
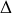 est un axe de symétrie d'ordre supérieur à 3
est un axe de symétrie d'ordre supérieur à 3
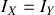 . Calculons
. Calculons
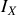 :
: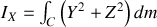
Pour mener le calcul, il faut découper le cylindre en ``tranches'' parallèles au plan
 et d'épaisseur
et d'épaisseur
 . Chaque tranche est un parallélépipède rectangle d'épaisseur
. Chaque tranche est un parallélépipède rectangle d'épaisseur
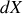 de longueur
de longueur
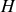 et de largeur
et de largeur
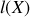 . La largeur
. La largeur
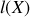 dépend de la position
dépend de la position
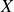 de la tranche dans le cylindre. Le calcul s'effectue en intégrant en premier lieu sur
de la tranche dans le cylindre. Le calcul s'effectue en intégrant en premier lieu sur
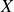 et
et
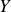 puis sur
puis sur
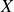 . Comme le cylindre est homogène, l'élément de masse
. Comme le cylindre est homogène, l'élément de masse
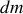 vaut
vaut
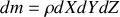 .
.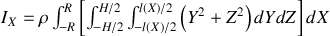
Or
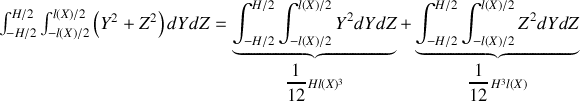
Soit
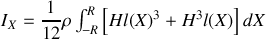
la largeur
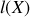 est la longueur d'une corde d'un cercle de rayon
est la longueur d'une corde d'un cercle de rayon
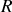 à une distance
à une distance
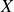 du centre du cercle, on en déduit la relation
du centre du cercle, on en déduit la relation
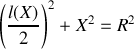 soit
soit
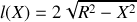 d'où
d'où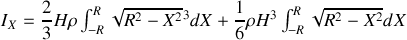
Les calculs se simplifient en posant
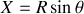 ainsi
ainsi
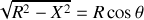 et
et
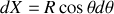 de sorte que :
de sorte que :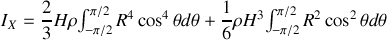
Pour calculer les intégrales, il faut linéariser les cosinus
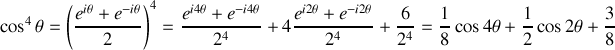
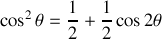
soit
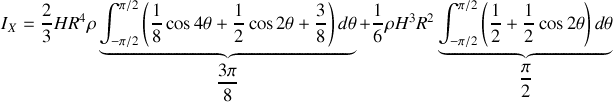
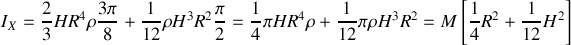
Le calcul de
 est plus rapide :
est plus rapide :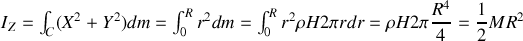
Le tuyaux possède le même centre de gravité et les mêmes axes de symétrie que le cylindre précèdent. Comme pour la balle creuse, on peut imaginer le tuyau comme composé d'un cylindre plein de rayon
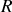 auquel on retire un cylindre de rayon
auquel on retire un cylindre de rayon
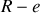 . Cela donne pour les moments principaux en appelant
. Cela donne pour les moments principaux en appelant
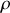 la densité :
la densité :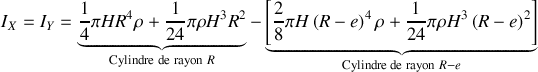
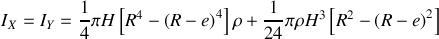
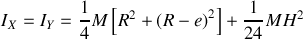
où
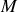 est la masse du tuyau
est la masse du tuyau