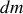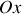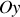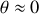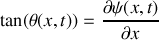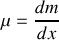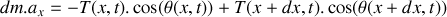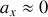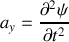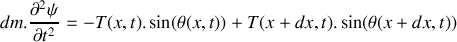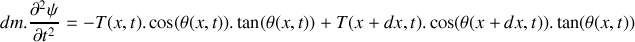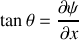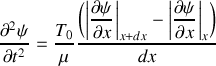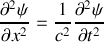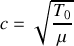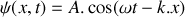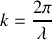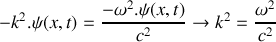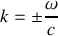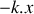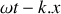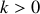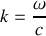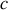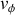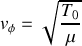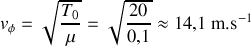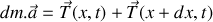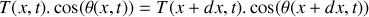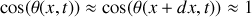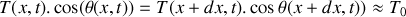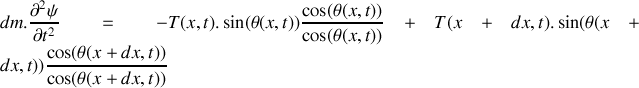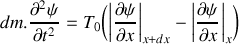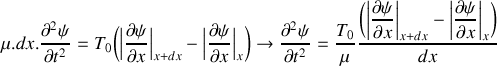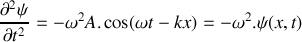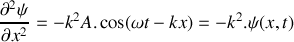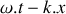Énoncé
Une corde homogène et inextensible de masse linéique
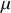 est tendue horizontalement avec une tension constante
est tendue horizontalement avec une tension constante
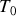 . Déplacée de sa position d'équilibre, la corde acquiert un mouvement décrit par le déplacement quasi-vertical
. Déplacée de sa position d'équilibre, la corde acquiert un mouvement décrit par le déplacement quasi-vertical
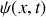 , mesuré à partir de la position d'équilibre. À l'instant
, mesuré à partir de la position d'équilibre. À l'instant
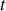 , la tension
, la tension
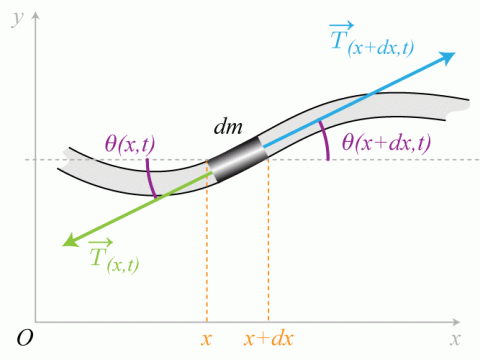
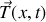 , exercée par la partie de la corde à droite d'un point
, exercée par la partie de la corde à droite d'un point
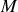 d'abscisse
d'abscisse
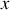 sur la partie gauche de la corde à gauche de
sur la partie gauche de la corde à gauche de
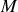 , fait un petit angle
, fait un petit angle
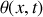 par rapport à l'horizontale (voir Figure 1). On négligera les effets de la force de pesanteur et des forces de frottements devant celui de la force de tension.
par rapport à l'horizontale (voir Figure 1). On négligera les effets de la force de pesanteur et des forces de frottements devant celui de la force de tension.
En considérant un tronçon infinitésimal de la corde compris entre
 et
et
 , montrer que
, montrer que
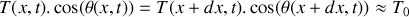
Montrer que le déplacement transversal
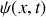 obéit à l'équation d'onde :
obéit à l'équation d'onde :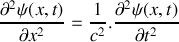
Exprimer c en fonction de
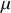 et
et
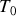 .
.La corde semi-infinie est le siège de la propagation d'une onde progressive sinusoïdale, de pulsation
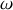 , se déplaçant dans le sens des
, se déplaçant dans le sens des
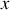 croissants telle que :
croissants telle que :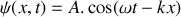 .
.3.a) En vérifiant que cette onde est effectivement solution de l'équation d'onde, donner l'expression de la relation de dispersion et de la vitesse de phase.
3.b) Calculer numériquement la vitesse de phase avec
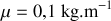 et
et
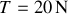 .
.