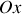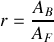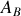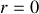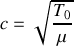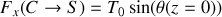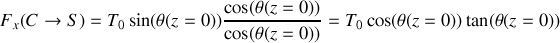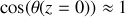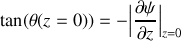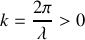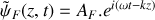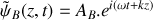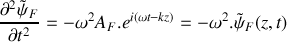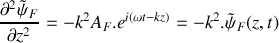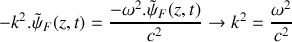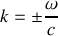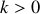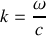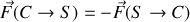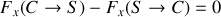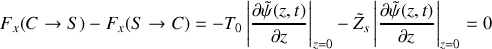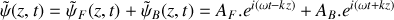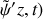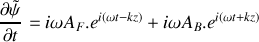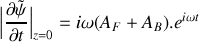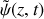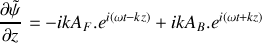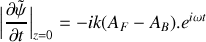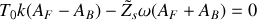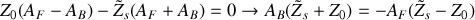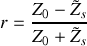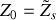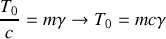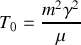Des ondes mécaniques transverses, générées par le pantographe, se propagent le long de câbles électriques utilisés dans l'alimentation des locomotives. En règle générale, la tension des câbles électriques est telle que la vitesse des ondes transverses est toujours supérieure à celle du train de sorte que le contact électrique entre le pantographe et le câble d'alimentation n'est jamais rompu. Même si l'onde transverse se déplace plus rapidement que le train, elle peut être partiellement réfléchie au niveau des points de suspension (caténaires), revenir vers le train et déconnecter le câble électrique du pantographe. Dans ce modèle simple, le système de suspension du câble électrique est assimilé à un anneau connecté par l'intermédiaire d'un ressort à un piston coulissant dans un cylindre. Il s'agit ici d'étudier la propagation des ondes le long du câble.

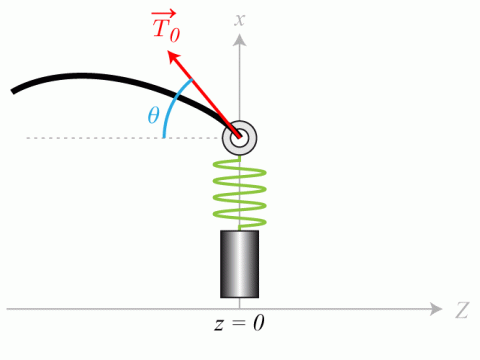
Comme l'indique la figure 1, la direction de propagation des ondes est notée 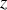et la direction transverse est notée 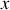. Le câble est attaché en 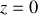à un point dont l'impédance mécanique complexe s'écrit 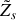. La propagation d'ondes mécaniques transverses le long du câble est régie par l'équation de d'Alembert : 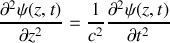où c est la vitesse de propagation de l'onde et 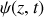représente l'amplitude transverse du mouvement du câble en 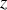, à l'instant 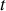. La masse linéique 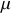du câble est constante et la force avec laquelle il est tendu à l'équilibre est aussi constante et notée 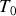. On négligera les effets de la force de pesanteur et des forces de frottements devant celui de la force de tension.

schéma représentant la propagation d'une onde transverse dans le câble

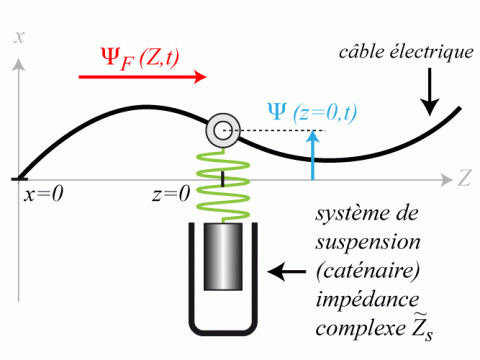
1. Montrer que la composante transverse de la force exercée par le câble sur le système de suspension (en 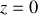) s'écrit :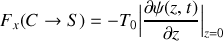

   

2. On suppose désormais qu'une onde progressive sinusoïdale se propage le long du câble électrique. Donner, en notation complexe, l'expression 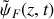d'une onde progressive sinusoïdale de pulsation 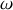et de nombre d'onde k se déplaçant dans le sens des 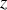croissants. Même question pour une onde progressive sinusoïdale 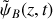se déplaçant dans le sens des z décroissants. Quelle est la relation de dispersion vérifiée pour ces deux ondes?

3. L'onde résultante se propageant le long du câble est la superposition d'une onde progressive sinusoïdale se déplaçant dans le sens des 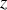croissants et d'une onde progressive sinusoïdale se déplaçant dans le sens des 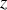décroissants, cette dernière onde étant issue de la réflexion de la première au niveau du système de suspension. Dans ces conditions, on a 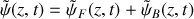. Sachant que l'impédance mécanique du câble est définie par la relation 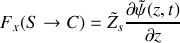et que l'impédance en 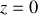s'écrit 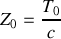, déterminer l'expression du coefficient de réflexion en amplitude du système de suspension.

4. En utilisant le résultat obtenu à la question 3) et sachant que l'impédance au niveau de la caténaire s'écrit 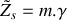avec m la masse et 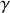le taux d'amortissement du ressort de la caténaire, donner l'expression, en fonction de 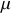, 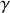et m, de la tension 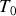à donner au câble pour que les ondes ne se réfléchissent pas au niveau des points de suspension.