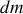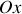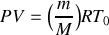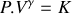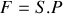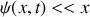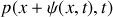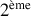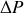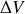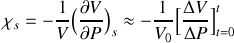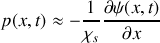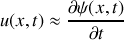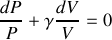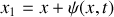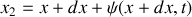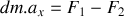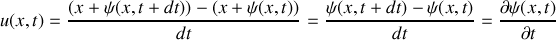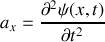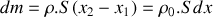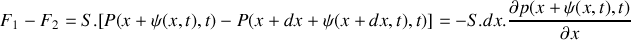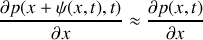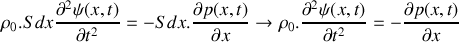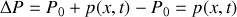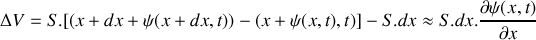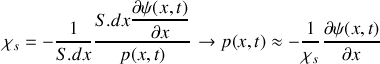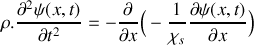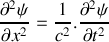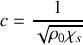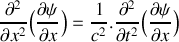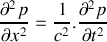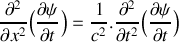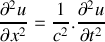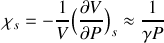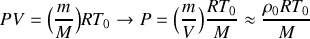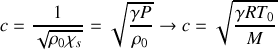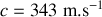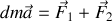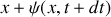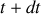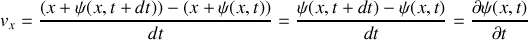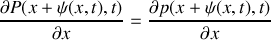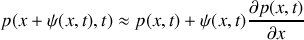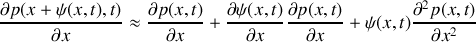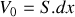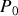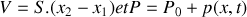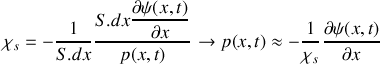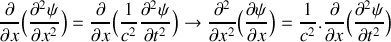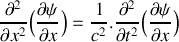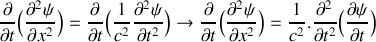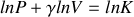Propagation d'une onde acoustique dans un fluide homogène. - Propagation d'une onde acoustique dans un fluide homogène.

Propagation d'une onde acoustique dans un fluide homogène.

Propagation d'une onde acoustique dans un fluide homogène.

Propagation d'une onde acoustique dans un fluide homogène.

Énoncé

Un tuyau cylindrique de longueur infinie et de section constante 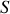, contient un fluide qui, au repos, est à la pression 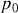, à la température 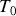et à une masse volumique .

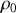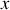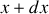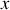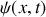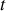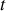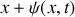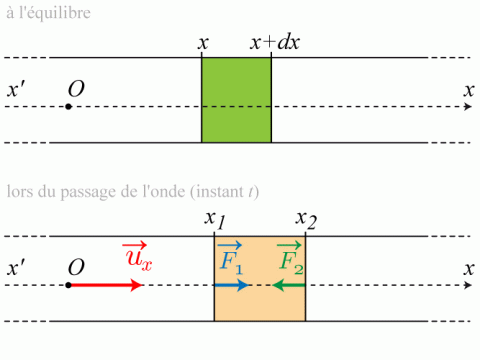
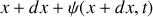On considère une tranche de fluide qui, au repos, est située entre les abscisses et . Le passage de l'onde acoustique s'accompagne d'un déplacement d'ensemble des molécules contenues dans le plan d'abscisse . Soit ce déplacement à l'instant . La tranche de fluide considérée se trouve ainsi à l'instant entre les plans d'abscisse et (voir figure 1).

schéma représentant la tranche de fluide au repos et à l'instant t

On notera :

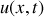, la vitesse de déplacement de la section d'abscisse 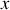à l'instant
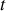
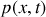, la surpression acoustique liée au passage de l'onde en 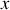à l'instant 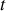. Ainsi la pression s'écrira
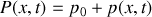
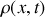, la masse volumique du fluide à l'abscisse 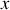à l'instant .

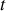On se limitera aux mouvements de faibles amplitudes : le déplacement particulaire 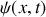, la surpression acoustique 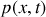, la variation de la masse volumique 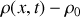et leurs dérivées peuvent être considérés comme des infiniments petits du premier ordre (on négligera dans la suite tous les infiniments petits d'ordre supérieur ou égal à deux). On négligera l'action de la pesanteur ainsi que toute viscosité ou frottements.

En raisonnant sur la tranche de fluide considérée et en précisant la loi utilisée, retrouver l'équation :
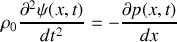
En supposant que l'évolution de la portion de fluide est isentropique, le coefficient de compressibilité isentropique d'un fluide est défini par :
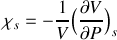où 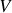est le volume du fluide et 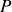sa pression.
Pour le fluide contenu dans le tuyau cylindrique, on supposera que 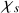est une constante.
Montrer que l'on peut écrire : .
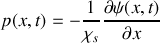a) En utilisant les résultats des questions 1) et 2), établir l'équation d'onde à laquelle satisfait la grandeur 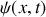. Exprimer 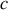(vitesse du son) en fonction de 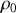et .
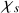b) Montrer que les grandeurs 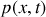et 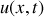satisfont à la même équation de propagation que .
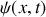Le fluide est de l'air considéré comme un gaz parfait :
- de 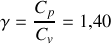(rapport des capacités calorifiques molaires à pression et à volume constants)
- de masse molaire
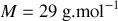
- de température
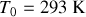
avec 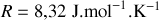(constante molaire des gaz parfaits).
Donner l'expression de 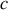en fonction de 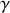, , 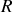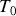et .
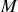Application numérique : calculer 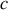dans l'air.

Aide simple

Aide détaillée

Rappel de cours

Méthodologie

Solution rapide

On pose et ( voir figure 2).

schéma représentant la tranche de fluide au repos et à l'instant t avec bilan des forces

En appliquant le principe fondamental de la dynamique sur la tranche de fluide et après projection sur l'axe horizontal , on obtient :

La vitesse acoustique est égale à :

En dérivant la vitesse, l'accélération s'écrit : .
Avec la conservation de la masse de la tranche de fluide, il vient :

Avec la force de pression et à constante, il vient :

Sachant que , on peut faire un développement au ordre de et en négligeant les termes du ordre, on obtient :

Alors :
Dans le cas de mouvements de faible amplitude, on peut écrire :

Il faut donc déterminer la variation de pression et de volume entre la tranche de fluide au repos et à l'instant :

et (voir question 1).
Alors :
a) En combinant les formules obtenues à la question 1) et 2), il vient :

En supposant que est une constante, on obtient finalement :
avec
b) En dérivant par rapport à l'équation d'onde obtenue à la question 3.a) et en supposant que les dérivations par rapport à et commutent, on a :
Avec (voir question 2) et constante, on obtient :

De la même façon en dérivant par rapport à , il vient :
avec (voir question 1), on obtient :
a) Pour un gaz parfait lors d'un transformation isentropique : où est une constante. En dérivant, il vient .
D'où où est la pression totale.
De plus, pour un gaz parfait de masse m à la température , on a :
pour de faibles variations de volume.
Alors :
b) A.N : , c'est la vitesse théorique du son dans l'air.

Solution détaillée

On pose et ( voir figure 2).

schéma représentant la tranche de fluide au repos et à l'instant t avec bilan des forces

En appliquant le principe fondamental de la dynamique sur la tranche de fluide, il vient :

Après projection sur l'axe horizontal , on obtient :

Le plan d'abscisse au repos est à l'abscisse à l'instant et à l'abscisse à l'instant . Alors, la vitesse acoustique est égale à :

En dérivant la vitesse, l'accélération s'écrit : .
Avec la conservation de la masse de la tranche de fluide, il vient :

avec la force de pression , il vient :

or avec constante, d'où :

Sachant que , on peut faire un développement au ordre tel que :

D'où :
En négligeant les termes du ordre, on obtient :
Alors :
Dans le cas de mouvements de faible amplitude, on peut écrire :

Il faut donc déterminer la variation de pression et de volume entre la tranche de fluide au repos et à l'instant .
- au repos : et la pression est
- à l'instant :
D'où :
(voir question 1).
Alors :
a) En combinant les formules obtenues à la question 1) et 2), il vient :

En supposant que est une constante, on obtient finalement :
avec
b) En dérivant par rapport à l'équation d'onde obtenue à la question 3.a) et en supposant que les dérivations par rapport à et commutent, on a :

En supposant que les dérivations par rapport à et commutent, on a :

Avec (voir question 2) et est constante, on obtient :

En dérivant par rapport à l'équation d'onde obtenue à la question 3.a), il vient :

En supposant que les dérivations par rapport à et et commutent, on a :

avec (voir question 1), on obtient :
a) Pour un gaz parfait lors d'un transformation isentropique : où est une constante. Ou encore : . En dérivant, il vient .
On peut alors réécrire le coefficient de compressibilité isentropique d'un fluide :
où est la pression totale.
De plus, pour un gaz parfait de masse m à la température , on a :
pour de faibles variations de volume.
Alors :
b) A.N : , c'est la vitesse théorique du son dans l'air.

Fin

Début