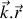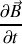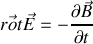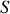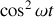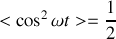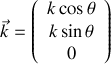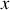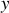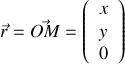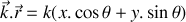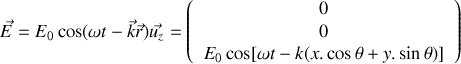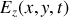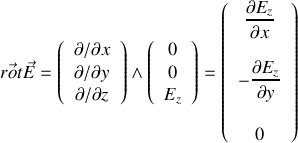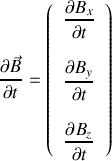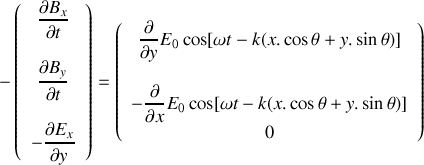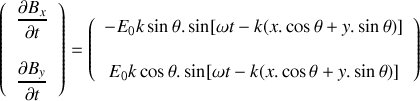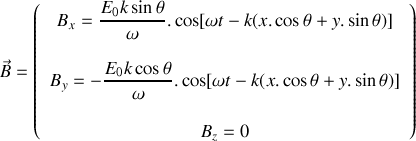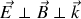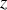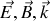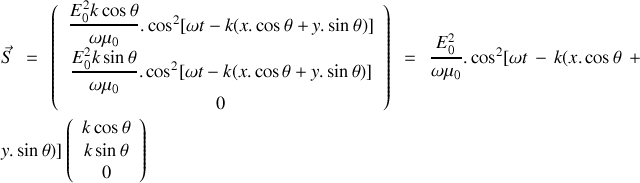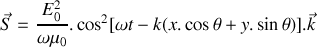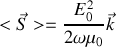Énoncé
On considère une onde électromagnétique plane, progressive, sinusoïdale et monochromatique de pulsation
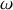 , se propageant dans le vide (caractérisé par la constante de la loi de Coulomb
, se propageant dans le vide (caractérisé par la constante de la loi de Coulomb
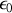 , la perméabilité magnétique du vide
, la perméabilité magnétique du vide
 et la célérité
et la célérité
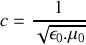 ). L'espace est rapporté à un repère cartésien
). L'espace est rapporté à un repère cartésien
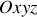 de base orthonormée. L'onde se propage dans le plan
de base orthonormée. L'onde se propage dans le plan
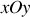 le long d'un axe faisant un angle
le long d'un axe faisant un angle
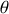 avec la direction
avec la direction
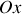 . Le vecteur champ électrique
. Le vecteur champ électrique
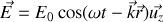 d'amplitude
d'amplitude
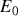 est parallèle à
est parallèle à
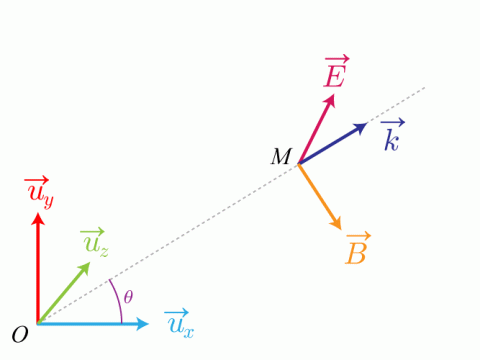
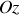 (voir figure 1).
(voir figure 1).
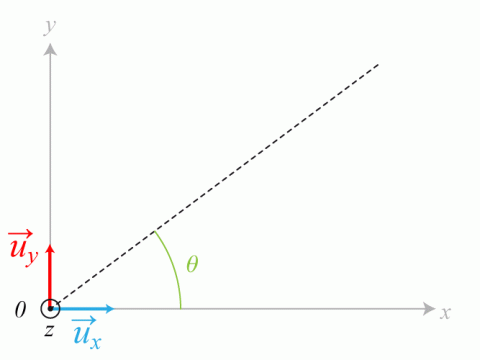
Écrire dans la base orthonormée
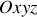 les composantes
les composantes
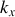 et
et
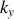 du vecteur d'onde
du vecteur d'onde
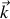 au point
au point
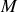 de coordonnées (
de coordonnées (
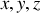 ) tel que
) tel que
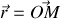 et à l'instant
et à l'instant
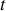 en fonction de son module
en fonction de son module
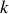 et de
et de
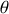 .
.Écrire dans la base orthonormée
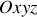 les composantes du vecteur champ électrique
les composantes du vecteur champ électrique
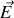 au point
au point
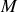 à l'instant
à l'instant
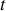 . En déduire, à l'aide des équations de Maxwell dans le vide (voir boîte à outils de l'exercice 11), les composantes en notation réelle du vecteur champ magnétique de l'onde
. En déduire, à l'aide des équations de Maxwell dans le vide (voir boîte à outils de l'exercice 11), les composantes en notation réelle du vecteur champ magnétique de l'onde
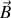 au point M.
au point M.Représenter sur un schéma les vecteurs
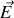 ,
,
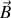 et
et
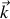 en justifiant leur orientation relative.
en justifiant leur orientation relative.Déterminer en notation réelle les composantes du vecteur de Poynting
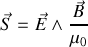 associé à l'onde électromagnétique en fonction de
associé à l'onde électromagnétique en fonction de
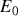 ,
,
 ,
,
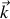 et
et
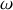 . En déduire sa valeur moyenne temporelle
. En déduire sa valeur moyenne temporelle
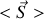 .
.