Réflexion d'une onde électromagnétique plane sur un diélectrique parfait. - Réflexion d'une onde électromagnétique plane sur un diélectrique parfait.

Réflexion d'une onde électromagnétique plane sur un diélectrique parfait.

Réflexion d'une onde électromagnétique plane sur un diélectrique parfait.

Réflexion d'une onde électromagnétique plane sur un diélectrique parfait.

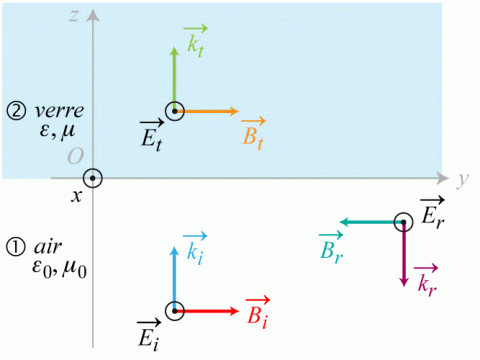
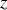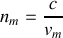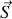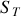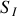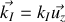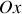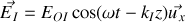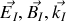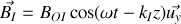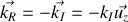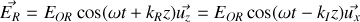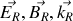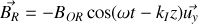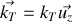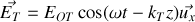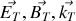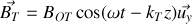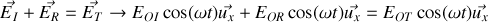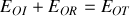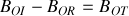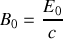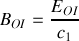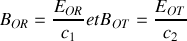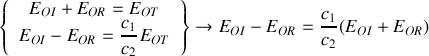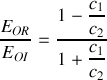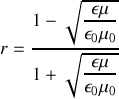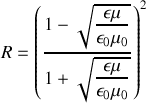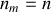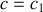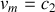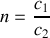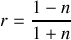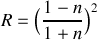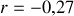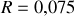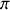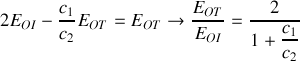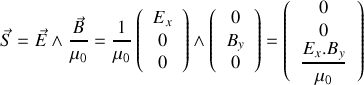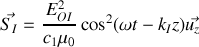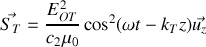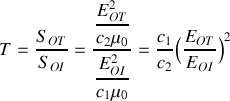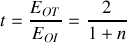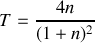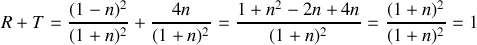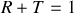Énoncé

On considère une onde électromagnétique plane, progressive, sinusoïdale et monochromatique de pulsation 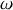, se propageant dans l'air (milieu 1). L'espace est rapporté à un repère cartésien 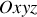de base orthonormée. L'onde se propage dans la direction 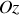normalement au dioptre plan séparant l'air (milieu 1) du verre (milieu 2). Le dioptre est placé à l'abscisse .

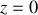On assimilera l'air au vide (caractérisé par la constante de la loi de Coulomb 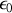, la perméabilité magnétique du vide 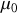et la célérité 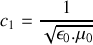) et le verre à un diélectrique parfait (caractérisé par la constante diélectrique 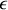et la perméabilité magnétique 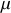telles que la célérité ).

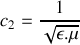Donner, en justifiant votre réponse, les expressions en notation réelle des champs électriques et magnétiques associées aux ondes incidentes, réfléchies et transmises. Préciser leur orientation relative et par rapport au sens de propagation en s'appuyant sur un schéma.
À l'aide des conditions de continuité caractérisant le passage de l'onde du milieu 1 vers le milieu 2, trouver le coefficient de réflexion en amplitude 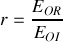et le coefficient de réflexion énergétique 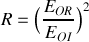. Exprimer ces coefficients en fonction de l'indice de réfraction du verre 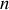. Calculer leurs valeurs pour 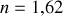. Le résultat est-il en accord avec le schéma de la question 1)?
À l'aide des conditions de continuité caractérisant le passage de l'onde du milieu 1 vers le milieu 2, trouver l'expression du coefficient de transmission en amplitude 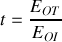en fonction de 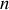. À partir de la conservation du flux du vecteur de Poynting 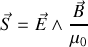au passage de l'onde du milieu 1 vers le milieu 2, on peut écrire le coefficient de transmission énergétique 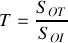. En considérant 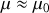, retrouver l'expression de 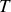en fonction de 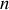et vérifier la conservation de l'énergie.

Aide simple

Solution détaillée

champs incidents :
L'onde se propage dans le sens des croissants, donc .
On choisit arbitrairement le champ électrique selon : .
( ) étant un trièdre direct, on a forcement : .
champs réfléchis :
À incidence normale, l'onde se propage dans le sens des décroissants après réflexion dans le même milieu 1, donc .
On a déjà choisit le champ électrique selon :
.
( ) étant un trièdre direct, on a forcement : .
champs transmis :
L'onde transmise se propage dans le sens des croissants dans le milieu 2, donc .
On a déjà choisit le champ électrique selon : .
( ) étant un trièdre direct, on a forcement : .

Voir figure 1.

schéma représentant les vecteurs E , B et k des ondes incidentes, réfléchies et transmises dans le repère orthonormé

2. La continuité du champ électrique en donne :

Soit :

La continuité du champ magnétique en donne :

Soit : .

Avec (voir exercice 11 : Propagation d'une onde électromagnétique plane dans le vide (1)) :

, avec (vitesse de phase dans l'air) et (vitesse de phase dans le verre).

On a alors le système d'équations :

Soit : . D'où :

L'indice de réfraction d'un milieu est défini par le rapport de la vitesse de phase dans le vide et de la vitesse de phase dans le milieu : . Ici, le milieu 1 est considéré comme le vide et le milieu 2 est le verre, , et , d'où .

Alors : et .

A.N. : et .

Dans ce cas, est négatif, donc les champs électriques incidents et réfléchis sont déphasés de . Ici, le schéma de la question 1) n'est donc pas correct : c'est le champ électrique qui change de sens à la réflexion alors que le champ magnétique ne change pas de sens.