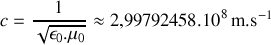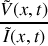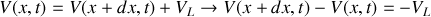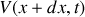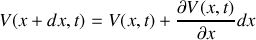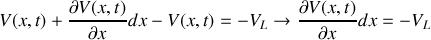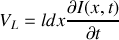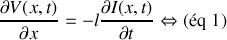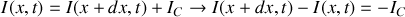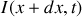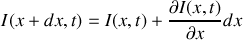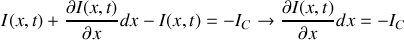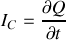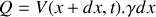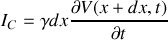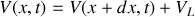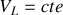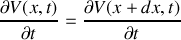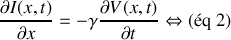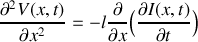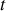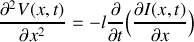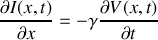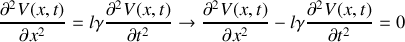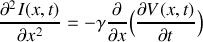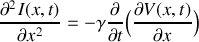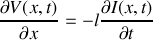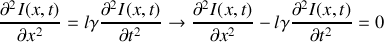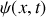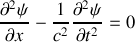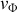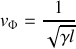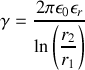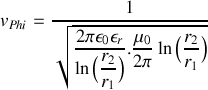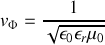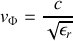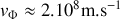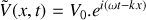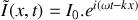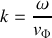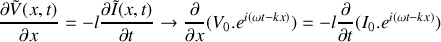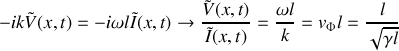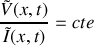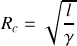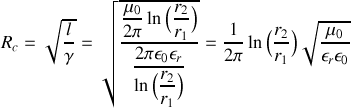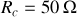Énoncé
Un câble coaxial est constitué des deux cylindres conducteurs, l'un creux (tresse métallique) et l'autre plein (fil électrique central), de même axe (d'où le nom de coaxial) et séparés par un isolant (gaine) de permittivité relative
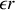. Le câble est caractérisé par sa capacité linéique l (le câble est comme un condensateur) et son coefficient d'auto-inductance l (le câble est comme une bobine).
On donne :
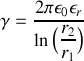et
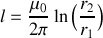avec
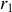le rayon du cylindre plein,
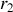le rayon du cylindre creux,
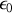la constante de la loi de Coulomb et
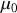la perméabilité magnétique du vide.
Par la suite, le câble sera supposé de longueur infinie et on négligera les effets de bord.
1. Un élément de câble de longueur infinitésimale
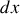peut être représenté schématiquement comme l'indique la figure 1.
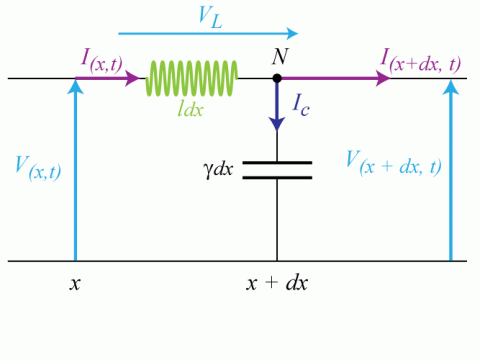
a) En appliquant les lois de l'électricité sur cet élément, trouver les deux équations aux dérivées partielles liant l'intensité
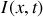et la tension
.
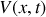b) En déduire les équations d'onde vérifiées par
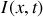et
.
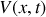c) Exprimer la vitesse de propagation des ondes de courant et de tension en fonction de
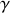et
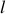, puis en fonction de
,
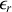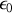et
.
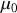d) Calculer sa valeur pour
.
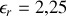2. On considère
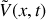une onde de tension sinusoïdale, progressive, de pulsation
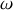, se propageant le long du câble dans le sens des
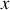croissants.
a) Donner sans démonstration les expressions, en notation complexe, de
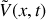et
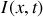vérifiant l'équation d'onde de la question 1.b).
b) Montrer qu'un tout point du câble le rapport
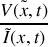est égal à une constante que l'on notera
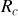. Que représente cette constante?
Calculer
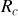avec
,
,
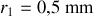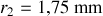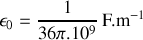et
.
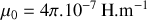