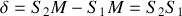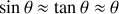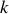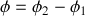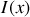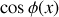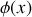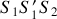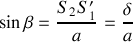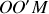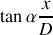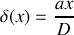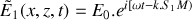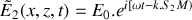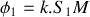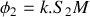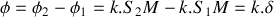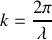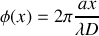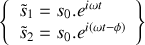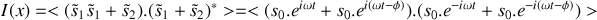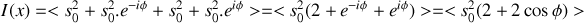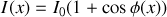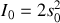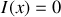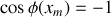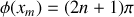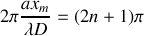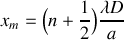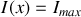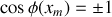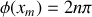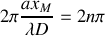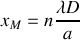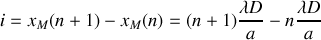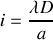Deux ondes 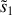et 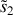"interfèrent" si à des endroits de l'espace l'intensité résultant de la superposition de ces ondes est différente de la somme des intensités de chaque onde arrivant seule : 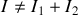. Trois conditions sont toutefois nécessaires pour qu'il y ait interférences :

• Il doit y avoir une zone commune de l'espace dans laquelle les deux ondes se propagent ; on parle de "zone d'interférences".

• Les deux ondes doivent avoir la même fréquence ; on parle d'ondes synchrones.

• Le décalage temporel des deux ondes doit être fixe (le déphasage de l'une par rapport à l'autre est constant) ; on parle d'ondes cohérentes.

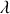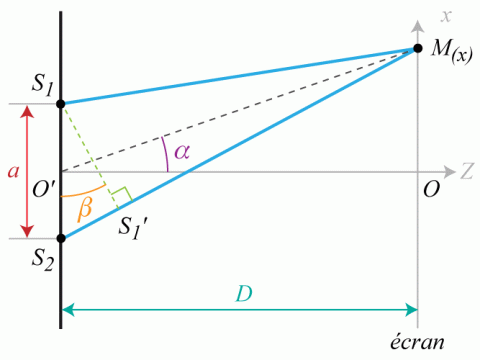
Le meilleur moyen de réunir ces conditions est de séparer une source unique en plusieurs sources secondaires, en réalisant par exemple l'expérience des fentes d'Young. Une source de lumière monochromatique, de longueur d'onde et de pulsation 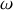, est placée avant une plaque percée de deux fentes de largeur très petite et de longueur très grande. Un écran est placé en suivant, parallèlement à la plaque. L'espace est rapporté à un trièdre orthonormé direct 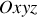attaché à l'écran, la lumière se propageant le long de l'axe 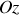et les fentes étant parallèles à l'axe .

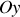Pour des raisons de symétrie, on se limitera donc à l'étude du phénomène dans le plan 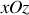. On note 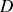la distance entre la plaque et l'écran et 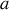la distance entre les fentes tel que 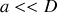. Le milieu entre la plaque et l'écran est considéré transparent, homogène et isotrope. Les rayons sont considérés comme respectant les conditions de Gauss.

1. Exprimer simplement, en fonction de 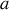, 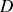et 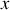, la différence de chemin optique parcouru (aussi appelée différence de marche) 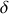entre un rayon issu de la fente 1 et un rayon issu de la fente 2 pour atteindre un point 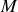de l'écran d'abscisse .

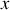2. Retrouver l'expression du déphasage 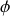entre deux ondes issues de la fente 1 et de la fente 2 en fonction de 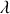, , 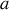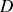et 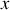. Écrire les ondes 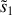et 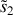en tenant compte de ce déphasage.

3. Déterminer l'intensité lumineuse résultante en 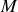en fonction de 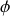sachant que :

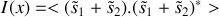   . En déduire les abscisses 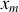pour lesquelles l'intensité est nulle et les abscisses 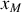pour lesquelles l'intensité est maximale.

4. Définir l'interfrange 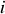et donner son expression en fonction 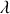, 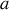et 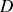. Calculer sa valeur pour 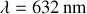, 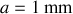et .
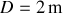