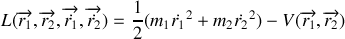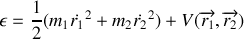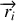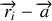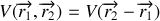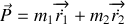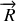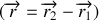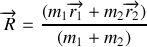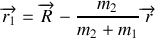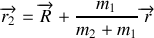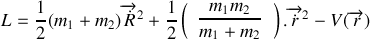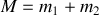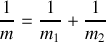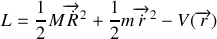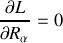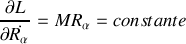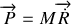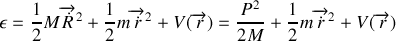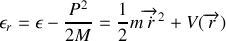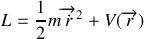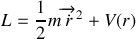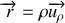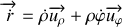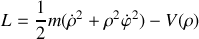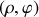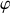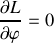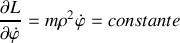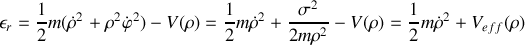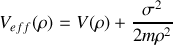Système à 2 corps et lois d'invariance - Système à 2 corps et lois d'invariance

Système à 2 corps et lois d'invariance

Système à 2 corps et lois d'invariance

Système à 2 corps et lois d'invariance

Énoncé

On considère 2 particules de masses 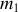et 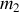en interaction l'une avec l'autre, mais isolées du milieu extérieur. Ces 2 particules sont repérées par leur rayons vecteurs 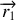et 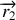. Nous supposerons que les forces d'interaction dérivent d'un potentiel .

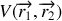Donner le nombre de degrés de liberté et le lagrangien du système. Nous allons utiliser les lois de conservation qui permettront de simplifier la résolution.
Les particules étant isolées, quelle intégrale première cela implique-t-il ?
L'isolement des 2 particules se traduit également par une invariance par translation d'espace. Réécrire le lagrangien en utilisant des coordonnées généralisées pertinentes.
Quelles sont les coordonnées cycliques qui apparaissent dans le lagrangien ainsi réécrit ? A quelle(s) loi(s) de conservation sont-elles associées ?
A partir de l'énergie totale du système exprimée dans ce jeu de coordonnées généralisées et de la loi de conservation précédemment établie, en déduire l'énergie du mouvement relatif et le lagrangien correspondant.
Le système étant isolé, il ne présente pas de direction privilégiée. Le lagrangien étant invariant par rotation autour de tout axe, le potentiel est également invariant par rotation, il ne dépend donc que de la distance 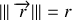entre les 2 particules.
On admettra que le mouvement du système est plan ; écrire le lagrangien dans le plan du mouvement défini par les coordonnées polaires ( 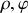). Ce lagrangien fait apparaître une coordonnée cyclique, à quelle intégrale première correspond-elle ?
Montrer que l'énergie mécanique relative établie en 5. peut s'écrire : 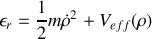où 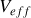est un potentiel effectif que l'on explicitera.

Aide simple

Solution détaillée

Il existe 6 degrés de liberté.
Le lagrangien s'écrit:
Le potentiel ne dépend pas explicitement du temps et le lagrangien non plus.
L'énergie est donc conservée: .
L'invariance par translation dans l'espace implique que le lagrangien est invariant dans le remplacement en . En particulier le potentiel ne dépend que du rayon vecteur relatif des 2 particules soit .
Cette invariance correspond à une autre intégrale première, la conservation de la quantité de mouvement totale : . Cette intégrale première nous suggère de travailler avec le centre de masse ( ) et le rayon vecteur relatif des 2 particules .

Exprimons le lagrangien en fonction de ces coordonnées avec et :

Introduisons la masse totale et la masse réduite
Les composantes du rayon vecteur sont des coordonnées cycliques.
et
On retrouve la conservation de la quantité de mouvement totale: .
Avec les vecteurs et , l'énergie s'écrit :

L'énergie totale est conservée, l'énergie cinétique du centre de masse est aussi conservée du fait de la conservation de la quantité de mouvement totale. La différence des 2 constantes donne l'énergie du mouvement relatif, soit: .
Pour déterminer l'équation du mouvement relatif, on utilisera le lagrangien suivant : .
Le problème initialement à six degrés de liberté se trouve ainsi ramené à un problème à 3 degrés de liberté ( ) avec en plus l'énergie mécanique qui est conservée.
L'invariance par rotation permet d'écrire le lagrangien sous la forme suivante: .
Le mouvement des 2 particules s'effectue dans le même plan défini par les coordonnées polaires ( ), et
; le problème se ramène désormais à un problème à 2 coordonnées généralisées .
est une coordonnée cyclique, .
, ce qui correspond à la conservation du module du moment cinétique (mouvement plan).
est un potentiel effectif comprenant le potentiel d'interaction entre les 2 particules et un potentiel centrifuge dont dérive la force centrifuge qui tend à éloigner les 2 particules.
Pour la résolution de l'équation du mouvement, se référer à l'exercice 'Mouvement dans un champ de force central'.

Fin

Début