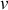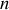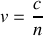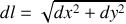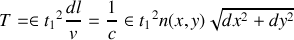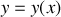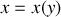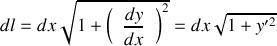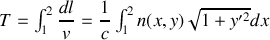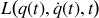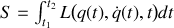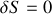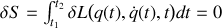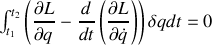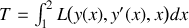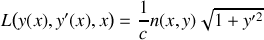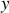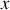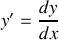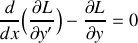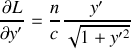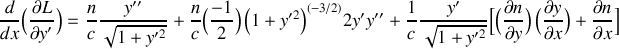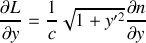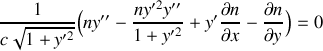Énoncé
Le principe de Fermat : entre 2 points, 1 et 2, le rayon lumineux suit la trajectoire qui prend le moins de temps (minimisation de la durée).
Considérons un milieu à deux dimensions
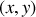, d'indice
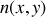pouvant dépendre de l'espace.
Donner la vitesse de la lumière dans ce milieu.
Calculer
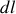l' élément de longueur de la trajectoire en fonction de
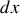et
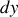.Ecrire la durée
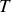du trajet entre deux points 1 et 2.Supposons que la trajectoire du rayon lumineux dans le plan soit décrite par une fonction
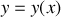. Exprimer l'élément de longueur en fonction de
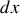et de
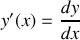.Ecrire l'action
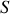d'un système mécanique décrit par une fonction de Lagrange
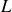dépendant de la coordonnée généralisée
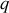, de sa dérivée au cours du temps
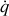et du temps
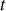. Donner l'équation du mouvement, dérivée du principe de moindre action de Hamilton.
Par une analogie directe entre l'action
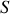du système mécanique et la durée
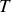du trajet du rayon lumineux, établir l'équation d'Euler-Lagrange correspondant à la minimisation de
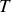.Dériver l'équation différentielle vérifiée par le rayon lumineux et montrer qu'elle se met sous la forme :
.
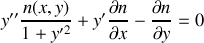