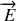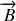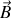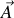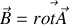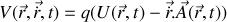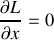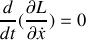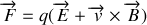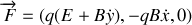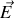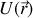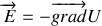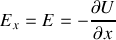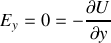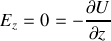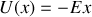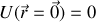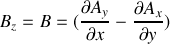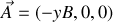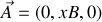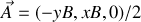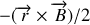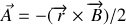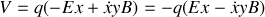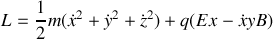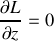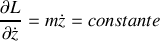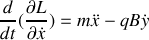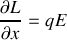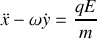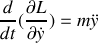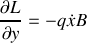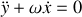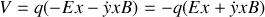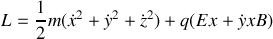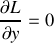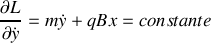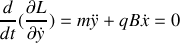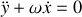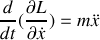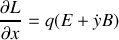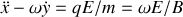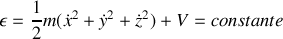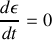Énoncé
Dans la base cartésienne, une particule de charge électrique
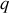est plongée dans un champ électrique
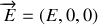et dans un champ magnétique
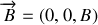uniformes et constants. Soient les coordonnées généralisées
.
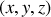Donner l'expression de la force de Lorentz qui est supposément la seule force agissant sur la particule.
Calculer le potentiel scalaire U(
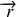).Montrer que l'on peut choisir un potentiel vecteur indifféremment de la forme
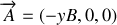ou
ou 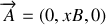encore
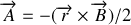.A l'aide de la première expression de
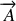, vérifier que le potentiel généralisé associé au champ électromagnétique s'écrit:
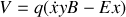. Ecrire le lagrangien de la particule dans le champ électromagnétique. .Que peut-on dire de la coordonnée
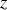? Donner l'intégrale première correspondante. Ecrire les équations de Lagrange pour les coordonnées
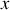et
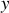en introduisant la pulsation cyclotron
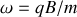.A l'aide de la seconde expression de
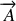, vérifier que le potentiel généralisé associé au champ électromagnétique s'écrit:
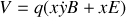. Ecrire le lagrangien de la particule dans le champ électromagnétique. Que peut-on dire des coordonnées
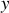et
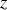? Donner les intégrales premières correspondantes. Etaient-elles prévisibles d'après la question précédente ? Ecrire les équations de Lagrange en fonction de la pulsation cyclotron
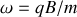. Le lagrangien ne dépend pas explicitement du temps, il existe une intégrale première associée à la translation dans le temps. Donner celle-ci.
