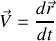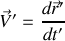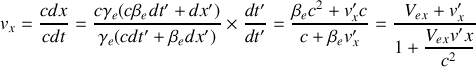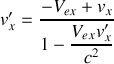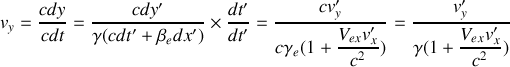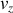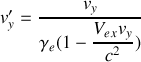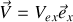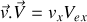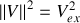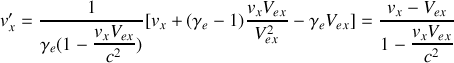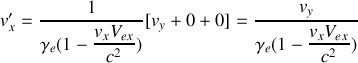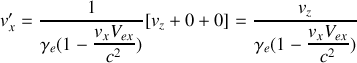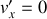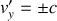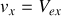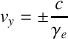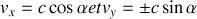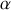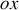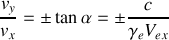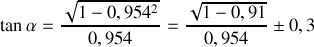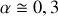Soient deux référentiels inertiels et 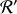ayant leurs axes parallèles. On note 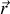et 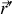les vecteurs positions d'une particule ponctuelle 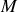repérée respectivement dans 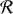et 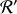. On note 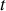et 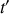les temps mesurés respectivement dans 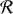et 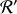. A l'instant 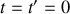, les deux origines 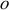et 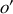des deux repères sont confondues. 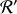est en translation uniforme par rapport à 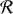dans la direction 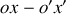avec une vitesse .

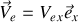1. A partir de dérivées adéquates des vecteurs positions, donner la définition des vecteurs vitesses 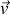et 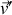  de la particule 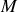mesurées dans 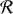et 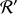respectivement.

2. Retrouver la loi de composition des vitesses, c'est-à-dire la relation entre les composantes de 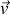, 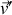et .

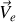3. Ecrire les composantes 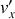, , 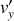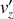à partir de la formule générale écrite sous forme vectorielle et vérifier que les expressions sont en accord avec les relations obtenues en 2. :

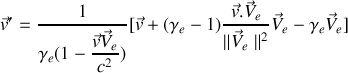
4. Dans le synchrotron Soleil de St Aubin en France, des électrons possédant une vitesse relativiste circulent dans un anneau et émettent des photons. Ces photons possèdent des propriétés remarquables. Parmi celles-ci figure la faible divergence du faisceau de photons émis, lorsque ces derniers sont recueillis dans le référentiel du laboratoire.

   Dans le référentiel attaché à un électron se propageant dans la direction 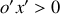, deux photons sont émis dans les directions 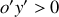et 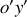< 0 (à 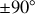de la direction du vecteur vitesse de l'électron). Sachant que cet électron est animé d'une vitesse 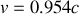par rapport au laboratoire, calculer l'angle \alpha que font les trajectoires des photons avec celle de l'électron pour un observateur du laboratoire.

   A.N. .
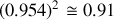