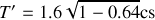Énoncé
Par rapport à un référentiel terrestre supposé inertiel, la distance Terre-Lune est de 384000
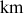. Une fusée effectue le voyage Terre – Lune à la vitesse
.
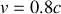Quelle est la durée du trajet pour un observateur terrestre ?
Quelle est la distance Terre – Lune pour un passager de la fusée ?
Quelle est la durée du voyage pour le passager ?
Cet exercice fait appel à la notion de dilatation des durées et de contraction des longueurs. Identifier les durées et les longueurs propre et/ou impropre pour chaque référentiel.
Dans un référentiel donné, utiliser la relation entre vitesse, durée et déplacement.
Le passager de la fusée doit faire le lien entre la longueur mesurée dans le référentiel terrestre et dans celui de la fusée.
Le passager de la fusée doit faire le lien entre la durée mesurée dans le référentiel terrestre et dans celui de la fusée.
Code grain : NLP_C_M06_G01.
La relation qui exprime la dilatation des durées est
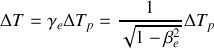avec
.
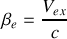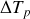est définie lorsque l'intervalle est de genre temps, c'est une mesure de durée entre deux événements localisés au même endroit, qui peut donc être effectuée avec une horloge.
Une mesure de longueur ne peut se faire que de manière simultanée. Il s'agira de plus d'une longueur propre si l'observateur (le référentiel) est immobile par rapport à la barre. La relation qui exprime la contraction des longueurs est
.
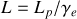Repérer les référentiels définis dans le problème et leur mouvement relatif. Si possible, associer des quadrivecteurs position à chaque événement du problème. Repérer les événements localisés ou non-localisés, pour chaque référentiel. Identifier les durées ou longueurs propres et impropres dans chaque référentiel. Revoir les notions liées à la dilatation des durées et à la contraction des longueurs, obtenues à partie des transformations de Lorentz.
.
.
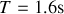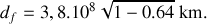
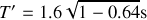Pour un observateur terrestre, la durée
du trajet dans le référentiel inertiel
est donnée par la relation
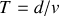où
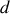est la distance propre Terre-Lune. La durée
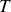est une durée impropre. A. N. :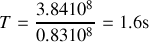
Un passager de la fusée (référentiel inertiel
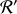) ne peut mesurer la distance Terre – Lune, soit
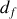, dans son repère mobile qu'en considérant deux événements simultanés
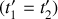. Il s'agira d'une longueur impropre. Ces deux événements, associés aux deux extrémités de la barre, ont pour coordonnées dans
:
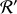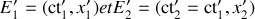. A l'aide de la transformation de Lorentz
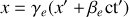, que l'on écrit pour chaque événement, on obtient :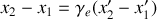
c'est-à-dire,
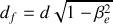
A.N. :
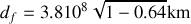
Pour un passager de la fusée, la durée
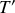du voyage dans le référentiel inertiel
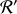est une durée propre, mesurée lorsqu'il est immobile :
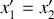.A l'aide de la transformation de Lorentz
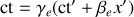, que l'on écrit pour chaque événement, on obtient :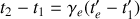
c'est-à-dire,
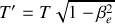
A.N. :
