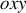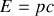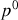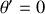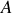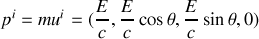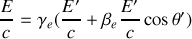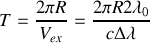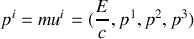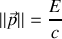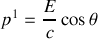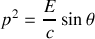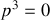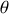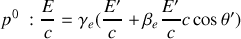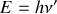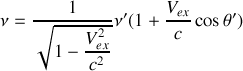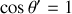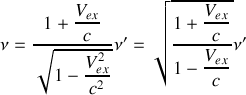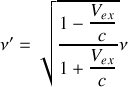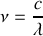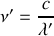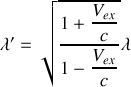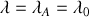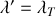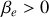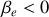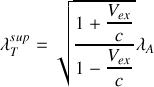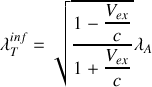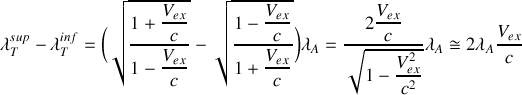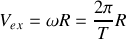Énoncé
Un photon d'énergie
(
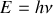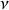est la fréquence du rayonnement) est émis dans un référentiel inertiel
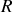. On souhaite calculer la fréquence
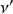qui sera mesurée dans un référentiel inertiel
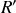, en translation rectiligne de vitesse
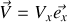suivant l'axe commun
,
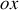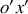des deux référentiels (
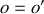en
).
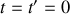a) Définir les composantes du quadrivecteur énergie-impulsion du photon dans
.
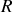b) A partir du quadrivecteur énergie-impulsion et des transformations de Lorentz associées, obtenir l'expression de l'effet Doppler-Fizeau longitudinal,
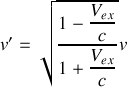
On observe depuis la Terre la radiation émise par un astre et dont la longueur d'onde est
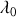dans le référentiel propre de la source. La résolution du télescope terrestre permet de dissocier les radiations provenant de deux points diamétralement opposés de l'équateur de l'astre. L'astronome en charge des mesures constate que les longueurs d'onde mesurées sur Terre à partir des deux points diffèrent d'une quantité
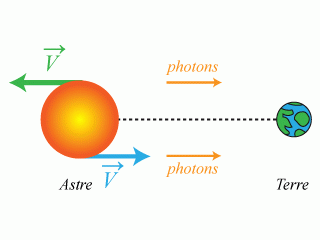
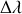. Cette observation lui permet de conclure que l'astre observé est en rotation (voir figure).
c) Obtenir l'expression de
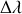en fonction de
,
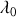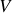et
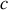, à l'approximation
.
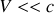d) Obtenir une expression de la période
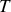de rotation de l'astre, en supposant connu son rayon
.
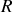