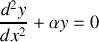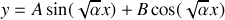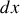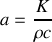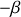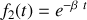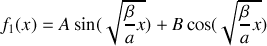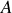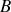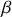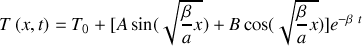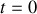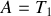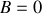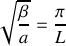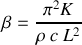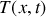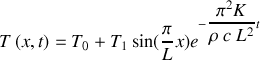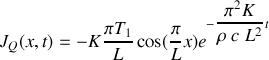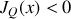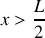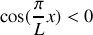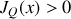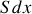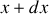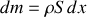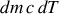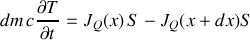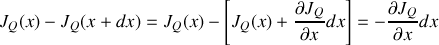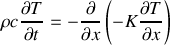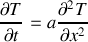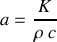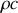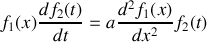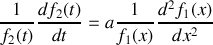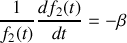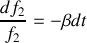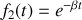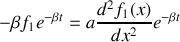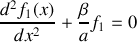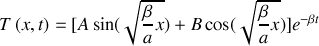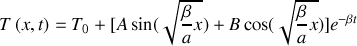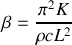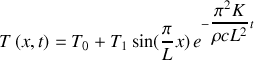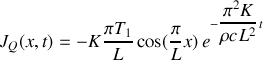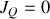Énoncé
Un barreau cylindrique métallique d'axe
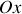, de longueur
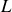, et de section, est caractérisé par sa chaleur massique
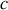, sa masse volumique
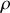et sa conductibilité thermique
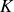. Ses caractéristiques sont supposées constantes et indépendantes de la température. Selon la loi de Fourier, la propagation unidirectionnelle de chaleur dans le barreau est proportionnelle en chaque point au gradient de température le long de celui-ci. La densité de flux de chaleur suivant
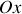à l'abscisse
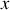, soit la quantité de chaleur qui traverse par unité de temps l'unité de surface du barreau s'écrit
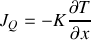
avec
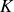la conductibilité thermique du métal en
.
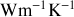En régime non permanent, la température du barreau est fonction de l'abscisse
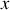et du temps
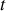considérés.Exprimer la conservation de l'énergie et établir l'équation de propagation de la chaleur sous la forme
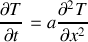
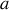s'appelle la diffusivité thermique. On l'exprimera en fonction de
,
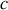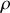et
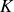.Déterminer la forme de la solution particulière
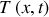de cette équation différentielle sous forme du produit d'une fonction de
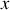par une fonction de
:
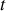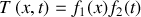
Le barreau cylindrique est plongé dans un milieu de température
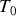maintenue constante. Sa température initiale est
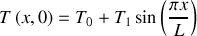. La chaleur dans le barreau va donc se propager depuis le centre plus chaud de la barre vers ses extrémité
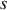.En écrivant la solution générale de l'équation de la chaleur comme la somme de la solution particulière
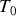et de la solution obtenue à la première question, déterminer la loi de distribution des températures
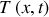dans le barreau métallique.En déduire l'expression de la densité de flux chaleur à l'instant
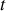et à l'abscisse
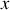. Vérifiez-vous le sens de propagation de la chaleur ?
