Énoncé
Montrer que la vitesse quadratique moyenne des molécules d'un gaz est égale à :
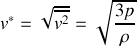
avec
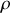 la masse volumique du gaz, et
la masse volumique du gaz, et
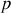 la pression du gaz.
la pression du gaz.Faire l'application numérique pour le dioxyde de carbone (
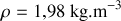 ), et pour
), et pour
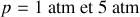 .
.
La pression
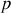 d'un gaz est le résultat des chocs des molécules sur les parois entourant le gaz. Il s'agit de compter toutes les molécules percutant la paroi pendant un intervalle de temps, et d'écrire leur changement de vitesse lors du choc comme résultat de la force exercée par la paroi sur elles. On considérera que leurs chocs sont élastiques, c'est à dire que l'énergie cinétique des molécules ne diminuent pas après le choc. A ces considérations, on ajoute l'hypothèse d'équipartition des vitesses dans le gaz.
d'un gaz est le résultat des chocs des molécules sur les parois entourant le gaz. Il s'agit de compter toutes les molécules percutant la paroi pendant un intervalle de temps, et d'écrire leur changement de vitesse lors du choc comme résultat de la force exercée par la paroi sur elles. On considérera que leurs chocs sont élastiques, c'est à dire que l'énergie cinétique des molécules ne diminuent pas après le choc. A ces considérations, on ajoute l'hypothèse d'équipartition des vitesses dans le gaz.
On raisonne d'un point de vue microscopique: la pression
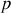 d'un gaz est le résultat des chocs des molécules sur les parois entourant le gaz. Pour chaque molécule, on écrit le principe fondamental de la dynamique dans son choc élastique avec la paroi, ce qui permet d'obtenir la force que chaque molécule exerce sur la paroi. L'ensemble de ces forces exercées pendant un temps donné sur
d'un gaz est le résultat des chocs des molécules sur les parois entourant le gaz. Pour chaque molécule, on écrit le principe fondamental de la dynamique dans son choc élastique avec la paroi, ce qui permet d'obtenir la force que chaque molécule exerce sur la paroi. L'ensemble de ces forces exercées pendant un temps donné sur
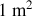 de paroi est égale à la pression dans le gaz. Pour obtenir le résultat, il faut compter toutes les molécules percutant la paroi pendant un intervalle de temps, et d'écrire leur changement de vitesse. On considérera que les chocs sont élastiques, c'est à dire que l'énergie cinétique des molécules ne diminuent pas après le choc.
de paroi est égale à la pression dans le gaz. Pour obtenir le résultat, il faut compter toutes les molécules percutant la paroi pendant un intervalle de temps, et d'écrire leur changement de vitesse. On considérera que les chocs sont élastiques, c'est à dire que l'énergie cinétique des molécules ne diminuent pas après le choc.
A ce calcul de la force moyenne exercée par les molécules, on ajoutera l'hypothèse d'équipartition des vitesses dans le gaz. Ces différentes étapes permettent de relier la pression dans le gaz à la vitesse quadratique moyenne des molécules de ce gaz.
Cours de référence: NLP_C_M10_G02
La théorie cinétique s'intéresse aux valeurs moyennes des grandeurs physiques pour un grand nombre de molécules. Les molécules d'un gaz ayant toutes la même masse, on peut par exemple définir la valeur moyenne
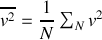
La vitesse quadratique moyenne ou vitesse efficace d'une molécule est
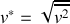
Pour chaque molécule, on peut décomposer la vitesse sur les trois axes d'un trièdre
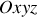 :
:
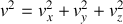
D'où
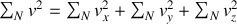 et
et
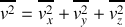
En raison de la répartition isotrope des vecteurs vitesse,
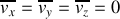 et
et
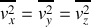 .
.
On en déduit
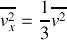
On écrit le principe fondamental de la dynamique pour chaque molécule dans son choc élastique avec la paroi, ce qui permet d'obtenir la force qu'elle exerce sur la paroi. On obtient la force moyenne exercée par les molécules en comptant le nombre de molécules heurtant la paroi pendant un intervalle de temps donné. La somme des forces exercées par m2 de paroi est égale à la pression dans le gaz. Une hypothèse importante est celle d'équipartition des vitesses dans toutes les directions.
La pression
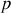 exercée par un gaz sur les parois qui l'entourent est résultat des chocs des molécules sur celles-ci. Suivant le principe fondamental de la dynamique, on peut écrire la variation de la vitesse d'une molécule suivant la direction normale à la paroi
exercée par un gaz sur les parois qui l'entourent est résultat des chocs des molécules sur celles-ci. Suivant le principe fondamental de la dynamique, on peut écrire la variation de la vitesse d'une molécule suivant la direction normale à la paroi
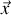 comme résultat de la force exercée par la paroi sur elle. C'est à dire une force opposée à celle qu'exerce cette molécule sur la paroi. Ainsi
comme résultat de la force exercée par la paroi sur elle. C'est à dire une force opposée à celle qu'exerce cette molécule sur la paroi. Ainsi 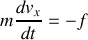
Donc, sur un intervalle de temps qui contient le choc,
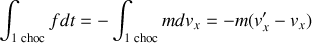
avec
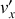 la composante normale à la paroi du vecteur vitesse après le choc. On peut considérer que le choc est élastique et que les vitesses suivant
la composante normale à la paroi du vecteur vitesse après le choc. On peut considérer que le choc est élastique et que les vitesses suivant
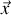 avant et après le choc sont égales en norme. Ainsi,
avant et après le choc sont égales en norme. Ainsi,
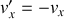 .
.La pression correspond à la valeur moyenne des forces exercées pendant un intervalle de temps
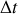 . Elles correspondent aux chocs des molécules contenues dans un cylindre de section unité et de hauteur
. Elles correspondent aux chocs des molécules contenues dans un cylindre de section unité et de hauteur
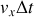 , donc de volume
, donc de volume
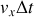 , et dont les composantes du vecteur suivant
, et dont les composantes du vecteur suivant
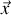 sont positives. Les vecteurs vitesse étant répartis uniformément dans tous les directions, les molécules pour lesquelles
sont positives. Les vecteurs vitesse étant répartis uniformément dans tous les directions, les molécules pour lesquelles
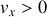 représentent la moitié des molécules présentent dans ce volume. On obtient
représentent la moitié des molécules présentent dans ce volume. On obtient 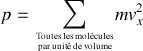
Par définition, et en raison de la répartition isotrope des vecteurs vitesse, on obtient
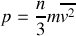
avec
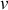 est la norme du vecteur vitesse d'une molécule. On reconnaît que
est la norme du vecteur vitesse d'une molécule. On reconnaît que
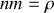 , et finalement
, et finalement 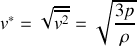
Applications numériques:
Dans le cas du dioxyde de carbone, et pour
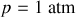 ,
,
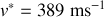 . Pour
. Pour
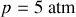 ,
,
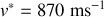
La pression
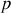 dans un gaz est égale à la pression exercée par ce gaz sur les parois qui l'entourent. Par définition, cette force perpendiculaire à
dans un gaz est égale à la pression exercée par ce gaz sur les parois qui l'entourent. Par définition, cette force perpendiculaire à
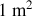 de paroi est le résultat des chocs des molécules sur celle-ci. Les molécules du gaz se déplacent à des vitesses différentes; il s'agit de faire l'inventaire des molécules percutant la paroi pendant un intervalle de temps, et de calculer la force moyenne exercée. Suivant le principe fondamental de la dynamique, on peut écrire la variation de la vitesse d'une molécule suivant la direction normale à la paroi
de paroi est le résultat des chocs des molécules sur celle-ci. Les molécules du gaz se déplacent à des vitesses différentes; il s'agit de faire l'inventaire des molécules percutant la paroi pendant un intervalle de temps, et de calculer la force moyenne exercée. Suivant le principe fondamental de la dynamique, on peut écrire la variation de la vitesse d'une molécule suivant la direction normale à la paroi
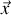 comme resultat de la force exercée par la paroi sur elle. C'est à dire une force opposée à celle qu'exerce cette molécule sur la paroi. Ainsi
comme resultat de la force exercée par la paroi sur elle. C'est à dire une force opposée à celle qu'exerce cette molécule sur la paroi. Ainsi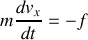
Donc, sur un intervalle de temps qui contient le choc,
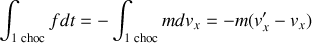
avec
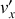 la composante normale à la paroi du vecteur vitesse après le choc.
la composante normale à la paroi du vecteur vitesse après le choc. On peut considérer que le choc est élastique et que les vitesses suivant
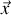 avant et après le choc sont égales en norme. Ainsi,
avant et après le choc sont égales en norme. Ainsi,
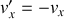 et
et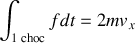
Alors,
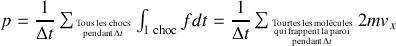
Comptons maintenant le nombre de molécules qui vont frapper l'unité de surface de la paroi pendant cet intervalle de temps
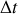 . Sont concernées les molécules contenues dans un cylindre de section unité et de hauteur
. Sont concernées les molécules contenues dans un cylindre de section unité et de hauteur
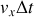 , donc de volume
, donc de volume
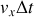 . Parmi toutes les molécules présentes dans ce volume, il ne faut considérer que celles dont la composante du vecteur suivant
. Parmi toutes les molécules présentes dans ce volume, il ne faut considérer que celles dont la composante du vecteur suivant
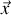 vaut
vaut
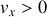 . Ainsi, ramené à l'unité de volume
. Ainsi, ramené à l'unité de volume
Les directions du vecteur vitesse étant réparties uniformément dans tous les sens, seule la moitié de ces molécules se dirigent vers la paroi. Donc
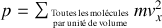
Par définition, la valeur moyenne du carré des vitesses suivant
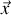 est
est
avec
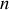 la densité volumique en molécules. Par ailleurs, en raison de la répartition isotrope des vecteurs vitesse, on a
la densité volumique en molécules. Par ailleurs, en raison de la répartition isotrope des vecteurs vitesse, on a
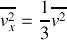 si
si
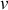 est la norme du vecteur vitesse d'une molécule.
est la norme du vecteur vitesse d'une molécule. Ainsi, on obtient
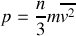
Enfin, le nombre de molécules par unité de volume fois la masse d'une molécule est égale à la masse volumique
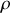 du gaz. On obtient donc finalement que la vitesse quadratique moyenne vaut
du gaz. On obtient donc finalement que la vitesse quadratique moyenne vaut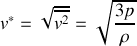
Applications numériques:
Considérons le cas du dioxyde de carbone. Pour
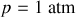 ,
,
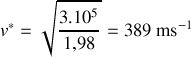 .
. Pour
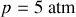 ,
,