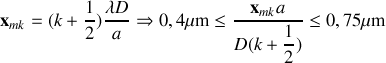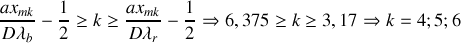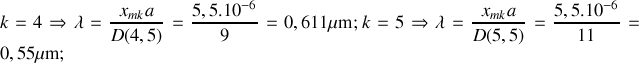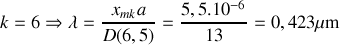Réponse 1
Les sources doivent être cohérentes c'est à dire même fréquence ou longueur d'onde et un déphasage entre elles constant dans le temps. On utilisant 2 sources identiques distinctes il n'y a pas cohérence de phase. Il faut obtenir 2 sources secondaires
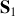et
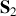issues d'une même unique source
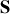(par division du front d'onde ou division d'amplitude). Par exemple éclairer 2 trous par une source
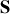. Les 2 trous se comportent alors comme 2 sources cohérentes en phase.
Réponse 2
a
Phénomène d'interférence : le long de
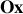, des franges alternativement brillantes et sombres, parallèles aux fentes
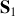et
.
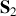b
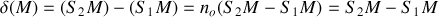est la différence de chemin optique entre les rayons issus des deux fentes et atteignant le point M.
En considérant
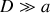, on a :
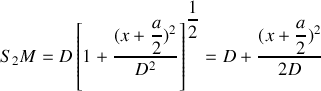et de même :
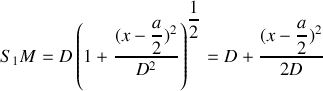
On a donc :
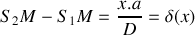
L'ordre d'interférence
(
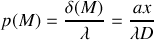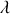la longueur d'onde dans le vide de la source).
L'onde issue de
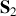arrive en
avec un retard dû à la propagation de l'onde. En choisissant l'origine des phases au niveau des sources, la phase en
est
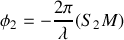. De même pour
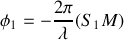. La différence de phase est :
.
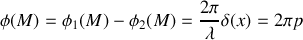c
Les deux sources étant identiques, on peut écrire, en
, la superposition des deux ondes issues des sources. On a :
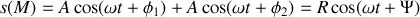. En utilisant la méthode de Fresnel ou en introduisant les complexes, on peut exprimer R :
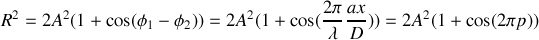
d
Franges brillantes si
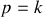, un entier relatif, ou bien
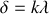(un nombre entier relatif de longueur d'onde) ou encore un déphasage
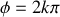
On a donc :
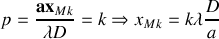. La frange centrale (
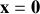, ordre d'interférence
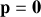) correspond à un maximum de lumière
Franges sombres si
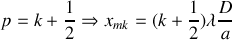
On appelle interfrange
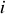la distance constante entre deux franges consécutives de même intensité (frange brillante par exemple) :
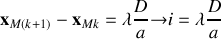. Elle dépend de la longueur d'onde.
e
Application numérique :
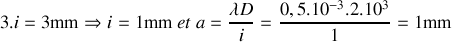
Réponse 3
La lame introduit un retard de phase pour
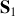par rapport à
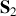. Le chemin optique dans la lame est :
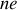. Dans l'air, on aurait eu
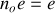. La différence de marche introduite est donc de:
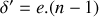. Le déphasage de
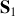par rapport à
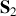est de
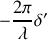
En
, les nouvelles phases sont:
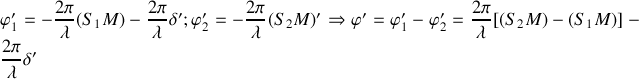
a donc:
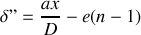
La figure d'interférence reste la même mais décalée vers les
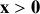. La frange centrale d'ordre
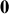correspond à
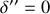soit
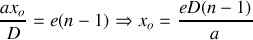
Application numérique :
.
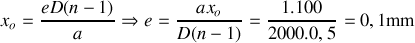Réponse 4
La source est maintenant une source de lumière blanche
.
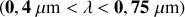a
Pour chaque longueur d'onde, on obtient une figure d'interférence. Sur l'écran, on observe la superposition des intensités de toutes les figures d'interférence (deux radiations de longueurs d'onde différentes ne peuvent pas interférer, on additionne donc les intensités).
On observe un frange centrale bien blanche, lumineuse (pour toutes les radiations, ordre 0 en
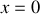) et quelques franges lumineuse blanches irisées (l'interfrange dépendant de la longueur d'onde, les radiation bleues donnent des franges moins écartées que les radiations rouges). En s'éloignant du centre, on observe rapidement un blanc dit d'ordre supérieur (il manque quelques radiations).
b
On obtient un spectre cannelé c'est à dire le spectre continu de la lumière blanche avec quelques raies noires (longueurs d'ondes manquantes) qui correspondent aux longueurs d'onde donnant une frange noire sur l'écran, au point considéré.
c
Raies manquantes pour:
