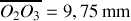Réponse 1
Une lentille divergente donne une image réelle que si l'objet est virtuel et situé entre le centre optique et le foyer objet. En utilisant les formules de conjugaison, et avec
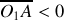 et
et
 , on obtient:
, on obtient:
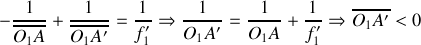
donc l'image est virtuelle et ne peut pas être sur le récepteur.
Réponse 2
a) La lentille
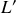 ne peut pas être divergente. En effet elle donnerait du point
ne peut pas être divergente. En effet elle donnerait du point
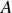 une image virtuelle qui deviendrait donc un objet réel pour la lentille
une image virtuelle qui deviendrait donc un objet réel pour la lentille
 . La lentille
. La lentille
 donnerait donc à son tour une image finale virtuelle.
donnerait donc à son tour une image finale virtuelle.
b) Soit
 le point image de
le point image de
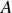 pour
pour
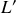 . Pour
. Pour
 ,
,
 est un objet qui donne une image finale réelle
est un objet qui donne une image finale réelle
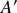 sur le récepteur. En remarquant que
sur le récepteur. En remarquant que
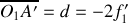 , on a:
, on a:
Pour le couple de points
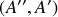 :
:
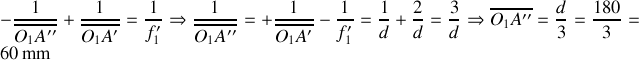
Pour le couple de points
 :
:
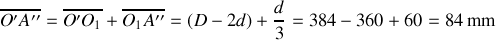 et
et

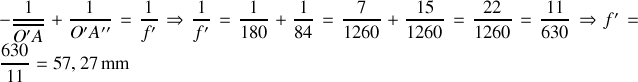
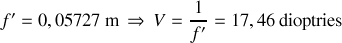
c) Le grandissement final est le produit des grandissements. On a:
 et
et
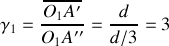 d'ou
d'ou
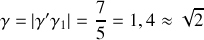
Un carré de côté
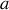 donne
donne
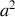 comme surface. Sur le récepteur on aura:
comme surface. Sur le récepteur on aura:
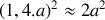 . La transformation est donc de
. La transformation est donc de
 en
en
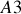 .
.
Réponse 3
Pour deux lentilles accolées, la vergence de l'ensemble est la somme des vergences. On a donc:
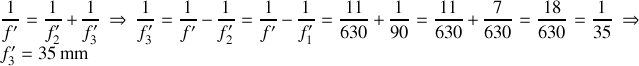 . La lentille est donc une lentille convergente.
. La lentille est donc une lentille convergente.
Réponse 4
Si nous inversons le sens de la lumière, nous nous retrouvons exactement dans la même configuration que précédemment. Le récepteur
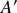 devient l'objet et le document
devient l'objet et le document
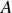 l'image.
l'image.
Le grandissement est donc de 1,4 c'est à dire que l'image
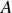 est 1,4 fois plus grande que l'objet
est 1,4 fois plus grande que l'objet
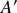 . En appliquant le principe du retour inverse de la lumière nous obtenons alors un grandissement inverse, soit de
. En appliquant le principe du retour inverse de la lumière nous obtenons alors un grandissement inverse, soit de
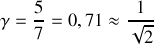 . Une surface de
. Une surface de
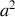 donnera sur le récepteur une surface de
donnera sur le récepteur une surface de
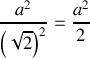 .La transformation est donc de
.La transformation est donc de
 en
en
 .
.
Réponse 5
Le grandissement transversal est

a) En appliquant le principe du retour inverse de la lumière nous devons obtenir un grandissement de
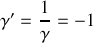 . Il faut donc que tout le dispositif soit symétrique par rapport au milieu (voir figure 1). La seule lentille convergente est
. Il faut donc que tout le dispositif soit symétrique par rapport au milieu (voir figure 1). La seule lentille convergente est
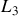 , elle doit donc être située au milieu de
, elle doit donc être située au milieu de
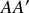 . Les lentilles divergentes identiques
. Les lentilles divergentes identiques
 et
et
 doivent être de part et d'autre de
doivent être de part et d'autre de
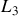 , à égale distance. Nous avons donc:
, à égale distance. Nous avons donc:
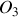 au milieu de
au milieu de
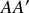 et
et
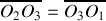
b) Nous avons :
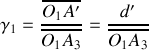 ,
,
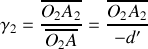 et
et
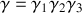
Si on applique le principe du retour inverse de la lumière, cela revient à remplacer
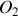 par
par
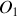 et
et
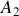 par
par
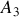 . Comme le dispositif est parfaitement symétrique par rapport au milieu cela implique que
. Comme le dispositif est parfaitement symétrique par rapport au milieu cela implique que
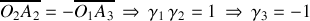
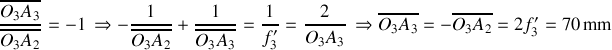 .
.
c)
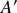 est l'image de
est l'image de
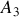 pour
pour
 : (avec
: (avec
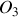 milieu de
milieu de
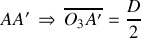 )
)
 et
et

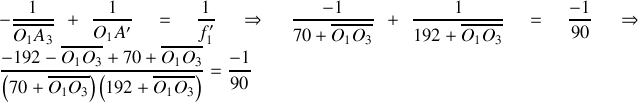

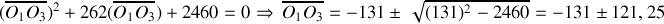
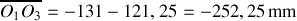 ou bien
ou bien
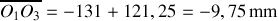
La première solution est impossible car
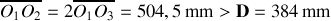 .
.
Finalement on a:
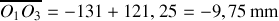 et
et