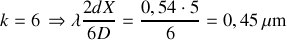Réponse 1
Soit le point
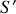 symétrique de
symétrique de
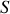 par rapport au plan du miroir :
par rapport au plan du miroir :
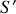 est l'image de
est l'image de
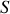 à travers le miroir. Tout rayon issu de
à travers le miroir. Tout rayon issu de
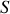 et se réfléchissant sur le miroir semble venir de l'image
et se réfléchissant sur le miroir semble venir de l'image
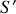 de
de
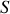 . Tout se passe comme si on avait 2 sources
. Tout se passe comme si on avait 2 sources
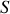 et
et
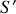 , cohérentes (car
, cohérentes (car
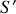 est l'image de
est l'image de
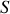 ). En un point
). En un point
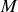 de l'écran deux rayons issus de
de l'écran deux rayons issus de
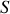 et
et
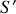 peuvent interférer. Le dispositif est équivalent au dispositif d'interférences des 2 fentes d'Young.
peuvent interférer. Le dispositif est équivalent au dispositif d'interférences des 2 fentes d'Young.
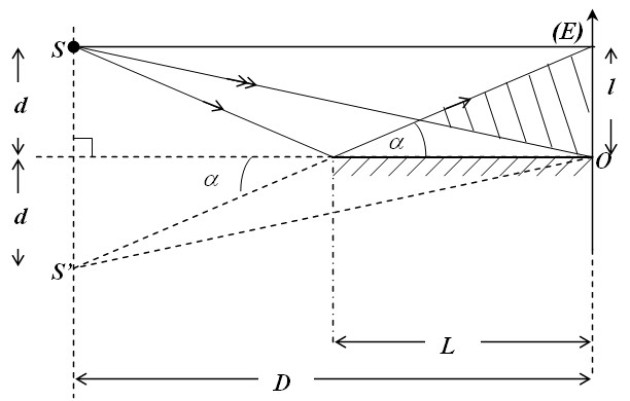
On observe des franges équidistantes alternativement brillantes et sombres et parallèles à la fente source. En considérant les rayons extrêmes passant par les bords du miroir et issus les uns de
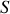 et les 2 autres de
et les 2 autres de
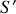 , la partie commune des deux faisceaux correspond à la zone d'interférences (voir figure 1) d'étendue
, la partie commune des deux faisceaux correspond à la zone d'interférences (voir figure 1) d'étendue
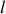 (délimité par l'angle
(délimité par l'angle
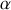 ).
).
Le phénomène d'interférence n'est pas localisé, il suffit de placer un écran n'importe où dans la zone d'interférences.
Réponse 2
La différence de marche
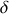 correspond à la différence de chemin optique entre les 2 rayons interférant en
correspond à la différence de chemin optique entre les 2 rayons interférant en
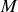 .
.
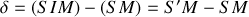
On se place dans les conditions où
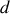 et
et
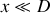 . Pour le calcul, il y a 2 méthodes :
. Pour le calcul, il y a 2 méthodes :
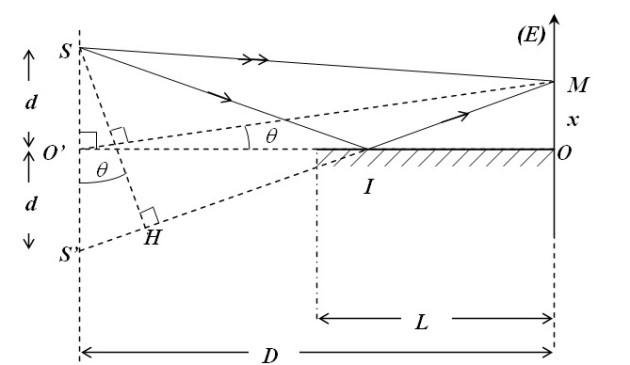
On peut considérer les rayons
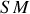 et
et
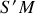 comme parallèles. Dans ces conditions, la différence de marche correspond à la distance
comme parallèles. Dans ces conditions, la différence de marche correspond à la distance
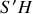 où
où
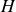
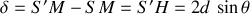
De même la droite
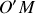 est parallèle aux deux rayons et donc fait le même angle
est parallèle aux deux rayons et donc fait le même angle
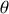 que
que
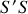 et
et
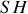 . On a donc :
. On a donc :
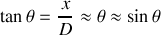 et donc
et donc
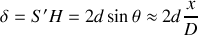 est le projeté de
est le projeté de
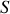 sur
sur
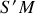 .
.
Sachant que le rayon réfléchi par le miroir subit un déphasage supplémentaire de
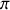 , la différence de phase
, la différence de phase
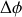 correspondante entre les deux rayons lumineux venant interférer au point
correspondante entre les deux rayons lumineux venant interférer au point
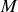 de l'écran
de l'écran
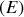 est :
est :
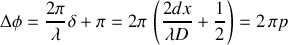 avec
avec
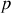 ordre d'interférence.
ordre d'interférence.
On exprime
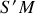 et
et
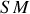 en utilisant le théorème de Pythagore :
en utilisant le théorème de Pythagore :
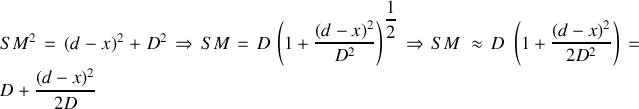
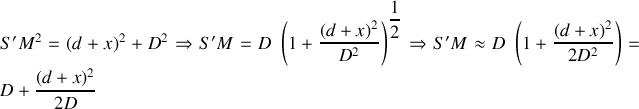
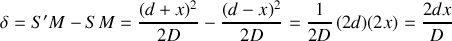
Réponse 3
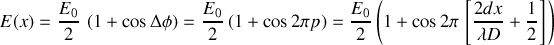
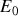 représente l'éclairement maximale (éclairement des franges brillantes)
représente l'éclairement maximale (éclairement des franges brillantes)
En
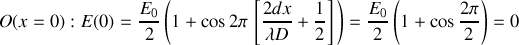 : la frange centrale est sombre.
: la frange centrale est sombre.
Réponse 4
Les franges brillantes sont définies pour
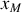 tel que l'ordre d'interférence soit un entier :
tel que l'ordre d'interférence soit un entier :
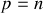 (avec
(avec
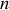 entier strictement positif,
entier strictement positif,
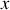 négatif est impossible avec ce montage contrairement avec les fentes d'Young)
négatif est impossible avec ce montage contrairement avec les fentes d'Young)
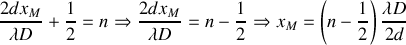 (1ère frange brillante :
(1ère frange brillante :
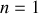 et
et
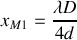 )
)
Pour les frange sombres :
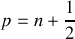 (avec
(avec
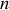 positif ou nul) :
positif ou nul) :
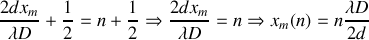
L'interfrange est la distance constante entre 2 franges consécutives de même nature.
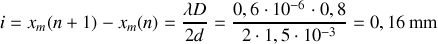
Réponse 5
5ème frange brillante :
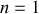 pour la 1ère frange et donc
pour la 1ère frange et donc
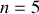 pour la 5ème
pour la 5ème
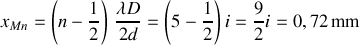
On a (voir figure 1 )
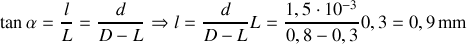
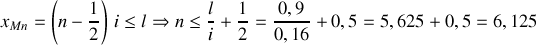 (6 franges brillantes visibles).
(6 franges brillantes visibles).
Réponse 6
Si on déplace la fente source très fine la figure d'interférence se décale. Une source étendue peut être considérée comme constituée d'une infinité de sources ponctuelles non cohérentes entre elles. Si on augmente la largeur de la fente source, chaque point source donne une figure d'interférence décalée les unes par rapport aux autres : il y a brouillage.
Réponse 7
La source est maintenant une source de lumière blanche
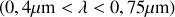 .
.
a) Pour chaque longueur d'onde, on obtient une figure d'interférence. Sur l'écran, on observe la superposition des intensités de toutes les figures d'interférence (deux radiations de longueurs d'onde différentes ne peuvent pas interférer, on additionne donc les intensités).
On observe en
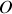 une frange sombre (pour toutes les radiations, frange sombre en
une frange sombre (pour toutes les radiations, frange sombre en
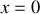 ) puis quelques franges lumineuse blanches irisées (l'interfrange dépendant de la longueur d'onde, les radiation bleues donnent des franges moins écartées que les radiations rouges). En s'éloignant du centre, on observe rapidement un blanc dit d'ordre supérieur (il manque quelques radiations).
) puis quelques franges lumineuse blanches irisées (l'interfrange dépendant de la longueur d'onde, les radiation bleues donnent des franges moins écartées que les radiations rouges). En s'éloignant du centre, on observe rapidement un blanc dit d'ordre supérieur (il manque quelques radiations).
b) On obtient un spectre cannelé c'est à dire le spectre continu de la lumière blanche avec quelques raies noires (longueurs d'ondes manquantes) qui correspondent aux longueurs d'onde donnant une frange noire sur l'écran, au point considéré.
c) Raies manquantes pour:
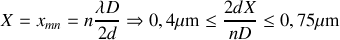
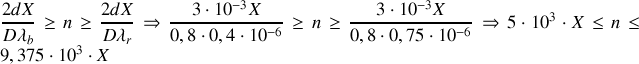
Pour
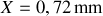 on a :
on a :
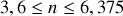 soit
soit
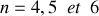
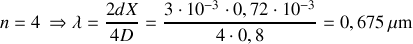 ;
;
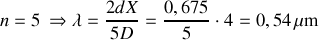 ;
;