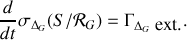L'égalité (1) implique l'égalité entre les résultantes des deux torseurs à savoir

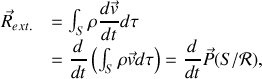
d'où l'expression du théorème de la résultante dynamique

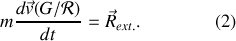
La deuxième relation donnée par (1) est l'égalité des moments des deux torseurs en un point fixe 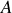de

ce qui peut se réécrire pour donner le théorème du moment cinétique en un point fixe de

Il est possible grâce au théorème de Koenig du moment cinétique d'obtenir une formule dérivée de (3) concernant le point 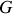dans le référentiel barycentrique

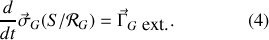
Dans le cas important de la rotation par rapport à un axe fixe (de directeur ) de , il vient par projection de (3) sur

où 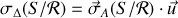et 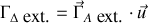. De même à partir de (4) dans le cas d'un axe , passant par 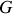et de direction fixe dans