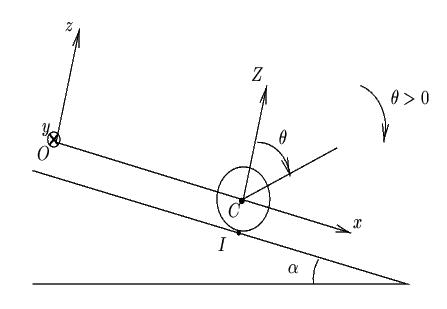
Soit donné un plan incliné
faisant un angle
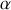avec le plan horizontal. On utilisera le référentiel
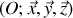, où
est parallèle à la ligne de plus grande pente du plan
,
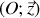est perpendiculaire à
et
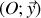forme avec les deux axes précédents un trièdre trirectangle direct. On notera
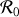ce référentiel.
Soit
une sphère creuse homogène, pesante, de masse
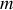, de rayon
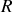, de centre
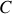, en contact avec le plan
. On désigne par
–
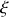l'abscisse du point
,
–
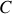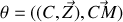où
est un rayon vecteur de la sphère contenu dans le plan
et
est parallèle et de même sens que
,
–
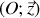le point de contact du plan avec la sphère.
La sphère reste en contact avec le plan
et le mouvement de
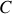a lieu dans le plan
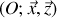. Le plan incliné est fixe et
est rigidement lié à ce plan.
Question 1
Première phase du mouvement :
est déposée sans vitesse initiale sur le plan
. A l'instant initial,
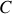est en
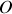. Le contact a lieu sans frottement.
a
Donner l'expression du moment d'inertie
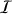de
par rapport à l'un quelconque de ses diamètres.
b
Ecrire les équations différentielles du mouvement. Quelle est la nature du mouvement dans cette phase ?
Question 2
Deuxième phase du mouvement : à l'instant
, la sphère arrive dans une zone où le coefficient de frottement de glissement avec
ne peut plus être négligé. On désignera par
–
le coefficient de frottement de glissement entre le plan et la sphère,
–
la réaction du plan
sur
.
On prendra comme nouvelle origine des temps l'instant
. On notera
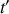les instants comptés à partir de cette nouvelle origine.
a
Etablir l'expression de
en fonction de
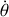et
.
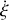Donner le signe de
à l'instant
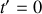, ainsi que la relation qui lie
et
tout au long de cette seconde phase.
b
Ecrire le théorème de la résultante cinétique et le théorème du moment cinétique. En déduire les valeurs de l'accélération du point
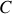et de l'accélération angulaire de
.
c
Quelle est la vitesse de
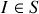à l'instant
?
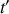A quelle condition (portant sur
et
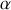) le glissement ne s'arrêtera-t-il jamais ?
d
On suppose que cette condition n'est pas satisfaite. A quel instant
le glissement cessera t- il ?
e
Entre les instants
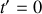et
, quel est le travail des forces de contact ? Montrer qu'on peut l'évaluer de deux manières différentes. On désignera par
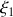la distance parcourue par le point
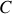pendant la seconde phase.
