Réponse 1
a
Par définition du moment d'inertie, on a
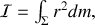
où
 est la distance au diamètre par rapport auquel on calcule
est la distance au diamètre par rapport auquel on calcule
 . Etant donnée la symétrie sphérique de
. Etant donnée la symétrie sphérique de
 , on peut laisser de côté la dimension transverse et on se ramène à l'intégration sur des couronnes circulaires de rayon
, on peut laisser de côté la dimension transverse et on se ramène à l'intégration sur des couronnes circulaires de rayon

où chaque point
 est affecté de la masse
est affecté de la masse
 de l'anneau qu'il représente soit
de l'anneau qu'il représente soit
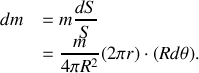
Dans ces conditions, comme
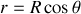 on obtient en reportant
on obtient en reportant
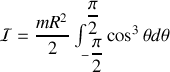
et finalement
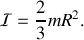
Il y avait dans ce cas précis une technique plus astucieuse : soient
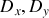 et
et
 trois diamètres de la sphère de directions respectives
trois diamètres de la sphère de directions respectives
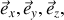 ces trois vecteurs formant un trièdre direct. Les moments d'inertie de la sphère par rapport à ces axes sont
ces trois vecteurs formant un trièdre direct. Les moments d'inertie de la sphère par rapport à ces axes sont
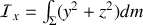 et permutations circulaires.
et permutations circulaires.
De plus, par symétrie, les trois diamétres sont équivalents, donc les trois moments sont égaux, et égaux au moment
 recherché. En les sommant, on a de ce fait
recherché. En les sommant, on a de ce fait

Comme
 est une constante, l'intégration des
est une constante, l'intégration des
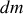 sur l'ensemble de la surface redonne la masse totale de la sphère, soit comme avec la précédente méthode
sur l'ensemble de la surface redonne la masse totale de la sphère, soit comme avec la précédente méthode
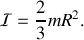
b
On applique la relation fondamentale de la dynamique (R.F.D.) à la sphère dans le repère
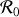 . En l'absence de frottements, cette dernière n'est soumise qu'à deux forces qui sont d'une part son poids
. En l'absence de frottements, cette dernière n'est soumise qu'à deux forces qui sont d'une part son poids
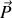 , et d'autre part la réaction du sol qui est normale :
, et d'autre part la réaction du sol qui est normale :
 . On exprime cette relation de la dynamique dans le repère
. On exprime cette relation de la dynamique dans le repère
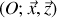 pour obtenir les équations différentielles du mouvement
pour obtenir les équations différentielles du mouvement

Au vu de ce système, on peut dire que la sphère effectue au cours de cette première phase un mouvement uniformément accéléré. Sa position au cours du temps est donnée par la double intégration de l'équation de

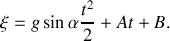
Les constantes introduites lors de ce calcul se déterminent au moyen des conditions initiales du mouvement qui sont

pour conduire à l'expression de l'abscisse du centre de gravité
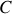 de la sphère durant cette première phase
de la sphère durant cette première phase

Réponse 2
a
Pour trouver la vitesse de glissement de la sphère sur le plan (c'est-à-dire comme le plan incliné est immobile dans le repère considéré, la vitesse du point
 appartenant à
appartenant à
 ) on utilise le torseur des vitesses de la sphère qui lie les vitesses de
) on utilise le torseur des vitesses de la sphère qui lie les vitesses de
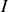 et de
et de
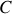 par la relation
par la relation

La vitesse du point
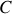 est donnée par
est donnée par
 , et le vecteur rotation instantanée, d'après la convention de signe choisie pour
, et le vecteur rotation instantanée, d'après la convention de signe choisie pour
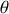 , a pour expression :
, a pour expression :
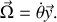
Le produit vectoriel s'effectue sans difficultés en prenant
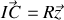 et conduit à
et conduit à
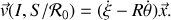
En l'absence de frottements, la sphère
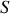 , initialement sans rotation autour de l'axe
, initialement sans rotation autour de l'axe
 est toujours dans cette configuration à l'issue de la première phase du mouvement, et donc
est toujours dans cette configuration à l'issue de la première phase du mouvement, et donc
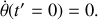
Notons avant de poursuivre qu'il peut paraître troublant de voir une bille avancer sans rouler... Pourtant cela n'a rien de surprenant pour quiconque est amateur de billard, et notamment de billard français pour lequel les boules sont plus massiques et donc se conforment assez bien aux lois de la mécanique sans frottements. Essayez donc de frapper une de ces boules exactement selon un diamètre horizontal, de manière à ne pas lui communiquer de rotation initiale, mais uniquement de la translation ; vous devriez constater que pendant quelques secondes la boule avance sans rouler !
Evidemment, les frottements sur le tapis ne sont dans ce cas de figure jamais nuls et la boule finit toujours par tourner, mais cela permet de se convaincre de la possibilité de la chose dans le cas où les frottements deviennent faibles —une bille d'acier poli sur un plan d'acier.
Au commencement de la seconde phase du mouvement, la vitesse de glissement se réduit à
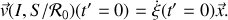
La vitesse de la sphère étant continue, sans quoi il faudrait faire intervenir des accélérations —donc des forces— infinies, ce qui n'a physiquement pas de sens,
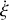 en
en
 est égal à
est égal à
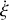 en
en
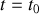 , c'est-à-dire que la vitesse est orientée vers le bas et la sphère descend. Les lois empiriques du frottement solide nous permettent d'en déduire le sens de la réaction tangentielle, et le lien qui existe entre les modules de
, c'est-à-dire que la vitesse est orientée vers le bas et la sphère descend. Les lois empiriques du frottement solide nous permettent d'en déduire le sens de la réaction tangentielle, et le lien qui existe entre les modules de
 et
et
 .
.
Le frottement de glissement s'oppose au glissement ce qui implique que la valeur algébrique de la réaction tangentielle vérifie
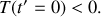
De plus il existe un coefficient
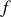 appelé coefficient de frottement de glissement tel que les modules des deux composantes de la réaction du sol sont liés par une relation de proportionnalité
appelé coefficient de frottement de glissement tel que les modules des deux composantes de la réaction du sol sont liés par une relation de proportionnalité

Les lois que nous venons de donner sont phénoménologiques : elles sont posées a posteriori de façon à rendre compte des phénomènes observés. Elles sont aussi appelées loi du glissement de Coulomb (voir les rappels de cours).
b
Tout comme à la question 1., appliquons la R.F.D., avec cette fois une réaction tangentielle non nulle. Un terme additionnel apparaît dans la première équation du système

Pour compléter ce jeu de deux équations, on applique comme le suggère l'énoncé, le théorème du moment cinétique par rapport à l'axe
 , passant par
, passant par
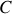 , et de vecteur directeur
, et de vecteur directeur
 . Dans ces conditions, en reprenant la notation de l'équation (5) des rappels de cours, on a la relation
. Dans ces conditions, en reprenant la notation de l'équation (5) des rappels de cours, on a la relation
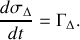
L'axe
 ainsi défini étant un diamètre de la sphère, on utilise le résultat de la question 1.a) pour exprimer le membre de gauche de la précédente équation
ainsi défini étant un diamètre de la sphère, on utilise le résultat de la question 1.a) pour exprimer le membre de gauche de la précédente équation
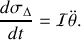
Le moment des forces par rapport à l'axe s'exprime quant à lui de la manière suivante (
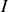 est le point d'application de la réaction du sol et
est le point d'application de la réaction du sol et
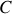 celui du poids)
celui du poids)
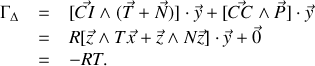
En recombinant les deux membres ainsi exprimés, on obtient une troisième équation

En utilisant (2) ainsi que les relations phénoménologiques sur le frottement de glissement, il vient
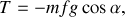
ce qui donne une fois inséré dans les équations (1) et (3) les expressions respectives de l'accélération du point
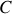 et de l'accélération angulaire
et de l'accélération angulaire
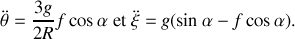
c
D'après l'expression de la vitesse de glissement trouvèe en 2.a), nous avons besoin de connaître non pas les accélérations, mais les vitesses à la fois angulaires et du point
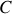 . Elles s'obtiennent en intégrant les résultats de la question précédente
. Elles s'obtiennent en intégrant les résultats de la question précédente
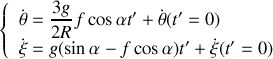
et nous permettent une fois reportées dans la formule de la vitesse de glissement d'obtenir
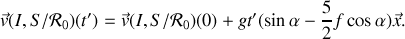
Les considérations précédentes nous ont donné pour valeur de la vitesse de glissement au commencement de la deuxième phase du mouvement

De ce fait, si le second terme de l'expression de la vitesse de glissement est également positif, cette dernière ne s'annulera jamais —elle s'annulera dans le cas contraire grâce au facteur
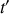 qui peut devenir infiniment grand. Cette condition de signe s'écrit
qui peut devenir infiniment grand. Cette condition de signe s'écrit
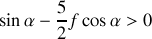
soit pour le coefficient de frottement de glissement
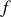 :
:

d
On se place dans le cas où le glissement va s'annuler au bout d'un temps fini
 . Cette condition s'exprime en utilisant la question précédente
. Cette condition s'exprime en utilisant la question précédente
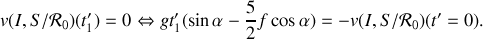
De l'expression trouvée en 1.b) pour la position du centre
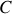 de la sphère, on déduit par simple dérivation temporelle
de la sphère, on déduit par simple dérivation temporelle
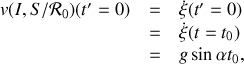
d'où pour

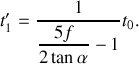
On peut remarquer à titre de vérification, qu'avec la condition prise sur
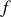 et
et
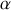 , ce temps
, ce temps
 est positif, c'est-à-dire que l'annulation de la vitesse de glissement a effectivement lieu.
est positif, c'est-à-dire que l'annulation de la vitesse de glissement a effectivement lieu.
e
Pour calculer le travail des forces de frottement entre les instants
 et
et
 , utilisons tout d'abord la méthode la plus générale à savoir le théorème de l'énergie cinétique. Celui-ci nous donne
, utilisons tout d'abord la méthode la plus générale à savoir le théorème de l'énergie cinétique. Celui-ci nous donne

Les forces en présence étant le poids de la sphère, qui dérive d'une énergie potentielle, et la réaction tangentielle du sol —la composante normale, partout normale au déplacement, ne travaille pas— cette expression se transforme en
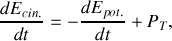
où
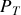 désigne la puissance des forces de contact. L'énergie potentielle de pesanteur a pour expression
désigne la puissance des forces de contact. L'énergie potentielle de pesanteur a pour expression
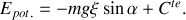
Finalement le théorème de l'énergie cinétique prend pour forme

Exprimons par ailleurs l'énergie cinétique du solide au moyen du théorème de Koenig qui stipule que
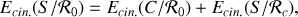
où
 est le référentiel du centre de masse. Autrement dit, l'énergie cinétique totale du solide se décompose en une énergie liée à la translation (premier terme), et une énergie liée à la rotation propre (deuxième terme).
est le référentiel du centre de masse. Autrement dit, l'énergie cinétique totale du solide se décompose en une énergie liée à la translation (premier terme), et une énergie liée à la rotation propre (deuxième terme).
Ainsi décomposée, l'énergie cinétique s'écrit
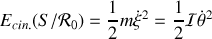
soit, après dérivation et substitution de
 :
:
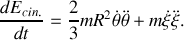
De plus, la question 2.b) nous donne pour les dérivées secondes
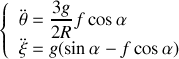
qui en reportant conduisent à
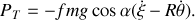
Pour le travail de la force, il ne reste plus qu'à intégrer en utilisant pour
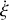 et
et
 les expressions temporelles trouvées au début de 2.c)
les expressions temporelles trouvées au début de 2.c)

soit en fonction du temps

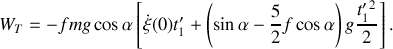
La deuxième méthode quant à elle consiste à calculer directement le travail de la force au moyen de l'expression littérale de celle-ci, obtenue à la question 2.b). En effet, le travail associé à un déplacement élémentaire s'écrit
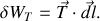
Le point délicat à ce niveau, est la façon dont s'exprime le déplacement élémentaire : il s'agit d'une distance sur laquelle la sphère a glissé ce qui comprend à la fois une distance suivant
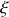 , mais aussi une distance due à la rotation —si la sphère tournait sur place, les forces de frottement travailleraient sans que pour autant l'abscisse
, mais aussi une distance due à la rotation —si la sphère tournait sur place, les forces de frottement travailleraient sans que pour autant l'abscisse
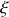 varie. L'expression du travail est alors
varie. L'expression du travail est alors

soit
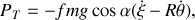
expression identique à celle obtenue avec la méthode précédente.




