On considère un gaz contenu dans un tuyau de symétrie axiale mais de section variable
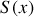 . Le gaz a une densité de masse locale
. Le gaz a une densité de masse locale
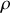 , une pression
, une pression
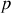 et un champ de vitesse locale
et un champ de vitesse locale
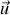 . On supposera que ces trois grandeurs ne sont dépendantes que de la coordonnée
. On supposera que ces trois grandeurs ne sont dépendantes que de la coordonnée
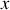 et du temps
et du temps
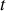 et que le champ de vitesse est principalement dans la direction de l'axe
et que le champ de vitesse est principalement dans la direction de l'axe
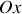 :
:
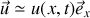 (voir la figure 7).
(voir la figure 7).
Question 1. Equation de continuité
a
Expliquer pourquoi les deux hypothèses précédentes sont fausses près de la paroi du tuyau.
b
Par un raisonnement direct, il est proposé d'établir l'équation de continuité exprimant la conservation de la masse sous la forme :
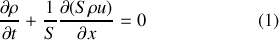
Pour ce faire, il est demandé de procéder comme suit. Considérer une couche de masse m comprise entre
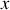 et
et
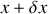 . Exprimer en fonction de
. Exprimer en fonction de
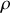 la variation de cette masse pendant
la variation de cette masse pendant
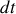 .
.
Calculer le flux de masse entrant et celui sortant de la couche pendant
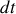 .
.
Postulant la conservation de la masse, déduire l'équation de continuité (1).
c
Retrouver l'équation (1) en utilisant l'équation de continuité générale établie dans le cours, à savoir :
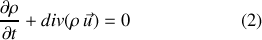
Pour cela, on se servira du théorème de la divergence appliqué à une couche d'épaisseur
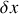 , en tenant compte du fait que la composante du champ de vitesse normale à la paroi s'annule sur cette paroi.
, en tenant compte du fait que la composante du champ de vitesse normale à la paroi s'annule sur cette paroi.
d
Conformément à la remarque de la question 1.a), montrer que l'équation (1) n'est effectivement compatible avec l'équation (2) que si l'on tient compte d'une petite contribution transverse du champ de vitesse.
Question 2. Dynamique du gaz
a
Montrer que l'équation d'Euler établie dans le cours (relation fondamentale de la mécanique pour un fluide inviscide) se réduit à :
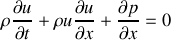
où la force de gravitation a été négligée. Expliquer ce que représente l'ensemble des deux premiers termes et le troisième terme de cette équation.
b
On suppose que le gaz est homogène et stationnaire à l'équilibre et que le mouvement décrit par
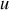 correspond à une petite perturbation. Ainsi on pose
correspond à une petite perturbation. Ainsi on pose
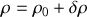 et
et
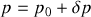 , où
, où
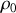 et
et
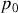 sont les valeurs d'équilibre constantes, avec
sont les valeurs d'équilibre constantes, avec
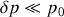 et
et
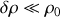 . Ecrire l'approximation linéarisée des équations de continuité et d'Euler portant sur
. Ecrire l'approximation linéarisée des équations de continuité et d'Euler portant sur
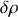 ,
,
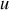 ,
,
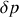 .
.
On suppose que la compression suit une loi de type adiabatique, à savoir que
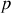 est proportionnel à
est proportionnel à
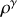 . écrire alors l'équation d'Euler en fonction de
. écrire alors l'équation d'Euler en fonction de
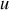 et
et
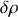 .
.
c
Montrer que la perturbation de densité évolue selon l'équation :
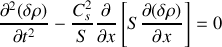
où
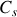 désigne la vitesse du son (
désigne la vitesse du son (
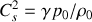 )
)
Montrer que la vitesse est gouvernée par une équation légèrement différente :
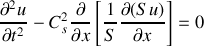
Question 3. Ondes dans un pavillon exponentiel
a
On considère un pavillon tel que
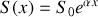 . Une vibration de pulsation
. Une vibration de pulsation
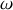 est imposée à l'entrée du pavillon et l'on cherche donc les solutions de l'équation de la vitesse sous la forme complexe :
est imposée à l'entrée du pavillon et l'on cherche donc les solutions de l'équation de la vitesse sous la forme complexe :
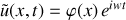
Montrer que la fonction complexe
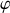 est solution de l'équation différentielle linéaire du second ordre :
est solution de l'équation différentielle linéaire du second ordre :
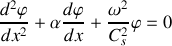
b
Quelles sont les solutions du problème dans le cas d'un tuyau cylindrique, c'est-à-dire
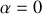 ? On note
? On note
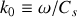 . Que représente
. Que représente
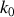 ?
?
c
Dans le cas d'un tuyau exponentiel (
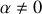 ), discuter de la nature des solutions et montrer notamment que les ondes sonores ne se propagent que pour
), discuter de la nature des solutions et montrer notamment que les ondes sonores ne se propagent que pour
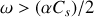 .
.
Montrer que les ondes ont une amplitude décroissant exponentiellement avec
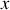 et calculer le nouveau nombre d'onde
et calculer le nouveau nombre d'onde
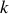 en fonction de
en fonction de
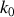 et
et
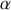 .
.
Donner l'expression générale de
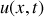 et l'expression de l'onde progressive.
et l'expression de l'onde progressive.
d
Ecrire la relation de dispersion sous la forme d'une équation reliant
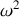 et
et
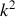 .
.
Quelle est l'expression de la vitesse de phase
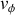 en fonction de
en fonction de
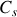 ,
,
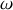 et
et
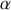 ?
?
Calculer la vitesse de groupe
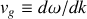 et vérifier que
et vérifier que
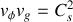 .
.
e
Calculer la densité d'énergie cinétique moyenne :
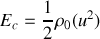 .
.
Comment varie alors
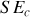 ? Commenter.
? Commenter.




