Réponse 1
a
Il est légitime de supposer que la forme de la vitesse loin des parois du tuyau est de la forme
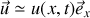 . Cependant, le tuyau étant immobile dans le référentiel d'étude, la vitesse du fluide normale à la paroi du tuyau doit être nulle. Près de la paroi,
. Cependant, le tuyau étant immobile dans le référentiel d'étude, la vitesse du fluide normale à la paroi du tuyau doit être nulle. Près de la paroi,
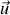 n'est donc plus parallèle à
n'est donc plus parallèle à
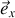 , afin de satisfaire la condition aux limites précédente. La composante transverse de la vitesse dépend alors fortement de la distance
, afin de satisfaire la condition aux limites précédente. La composante transverse de la vitesse dépend alors fortement de la distance
 à l'axe de symétrie du tuyau, puisqu'elle n'entre en jeu que dans une zone proche de la paroi du tuyau.
à l'axe de symétrie du tuyau, puisqu'elle n'entre en jeu que dans une zone proche de la paroi du tuyau.
L'apparition de cette composante transverse de la vitesse implique également que les champs de pression, de densité de masse et de vitesse dépendent de
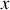 ,
,
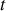 et
et
 près de la paroi.
près de la paroi.
Cependant, on peut estimer que les approximations faites dans le problème vis-à-vis de la dépendance des champs sont correctes, à partir du moment où l'on pourra négliger les effets de bords dˆus à la paroi, ce qui signifie que la section du tube est grande devant la zone proche de la paroi où les hypothèses de départ sont manifestement fausses.
Remarque : deux types de conditions aux limites peuvent être envisagés. Dans le cas d'un fluide visqueux, la vitesse s'annule au fur et à mesure que l'on se rapproche d'une paroi immobile. Dans un référentiel où la paroi est en mouvement, cette condition se traduit par :
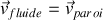
Dans la situation idéale d'un fluide non visqueux, c'est la composante normale à la paroi qui s'annule au voisinage de celle-ci :
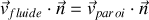
où
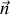 est un vecteur normal à la paroi au point considéré.
est un vecteur normal à la paroi au point considéré.
Cette condition traduit l'imperméabilité de la paroi au fluide. C'est cette condition qui a été adoptée ici, avec
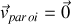 , conformément à l'hypothèse de viscosité nulle qui sera faite par la suite. Bien entendu, la viscosité d'un écoulement n'est jamais strictement nulle, mais elle peut être suffisamment petite pour que ses effets ne jouent que dans une couche limite confinée au voisinage immédiat de la paroi.
, conformément à l'hypothèse de viscosité nulle qui sera faite par la suite. Bien entendu, la viscosité d'un écoulement n'est jamais strictement nulle, mais elle peut être suffisamment petite pour que ses effets ne jouent que dans une couche limite confinée au voisinage immédiat de la paroi.
b
Soit une tranche
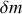 de fluide analogue à celle de la figure de l'énoncé. La variation de la masse du fluide contenue dans cette tranche est :
de fluide analogue à celle de la figure de l'énoncé. La variation de la masse du fluide contenue dans cette tranche est :
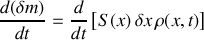
On en déduit :
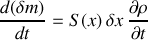
Le flux de masse entrant dans la couche par unité de temps est, par définition :
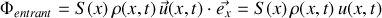
puisque la normale à la tranche de fluide est colinéaire à
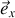 . De même, le flux de masse sortant par unité de temps est :
. De même, le flux de masse sortant par unité de temps est :
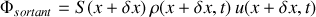
La variation de la masse de fluide contenue dans la tranche d'épaisseur
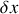 s'écrit de manière générale sous la forme :
s'écrit de manière générale sous la forme :

Dans le problème qui nous intéresse, l'égalité précédente se traduit par :
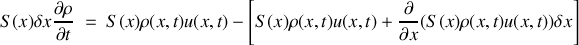
pour la tranche de fluide infinitésimale considérée. On obtient ainsi l'équation (1) recherchée :
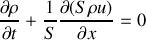
c
Etablissons tout d'abord l'équation de continuité (2) proposée : soit un volume (
 ) de fluide entouré par une surface fermée (
) de fluide entouré par une surface fermée (
 ). Pour ce volume de fluide, la conservation de la masse s'écrit sous la forme :
). Pour ce volume de fluide, la conservation de la masse s'écrit sous la forme :
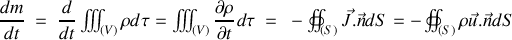
avec la normale à la surface (
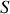 ) orientée vers l'extérieur,
) orientée vers l'extérieur,
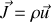 étant le vecteur densité de courant de masse. En appliquant le théorème d'Ostrogradsky (ou de la divergence), on arrive à :
étant le vecteur densité de courant de masse. En appliquant le théorème d'Ostrogradsky (ou de la divergence), on arrive à :
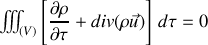
ce qui conduit, la démonstration précédente étant valable pour tout volume (
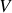 ) de fluide, à l'équation de continuité (2) :
) de fluide, à l'équation de continuité (2) :
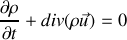
Dans le cas de la tranche de fluide comprise entre
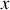 et
et
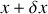 , l'application de l'équation de continuité conduit à :
, l'application de l'équation de continuité conduit à :
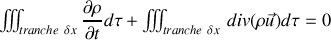
En appliquant le théorème de la divergence, on arrive, après intégration sur la tranche de fluide, à :
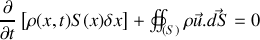
En développant cette dernière intégrale, on retrouve bien l'équation (1) puisque :
la normale à la surface est
 pour le plan
pour le plan
la normale à la surface est
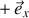 pour le plan
pour le plan
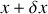
d'après les conditions aux limites dont nous avons parlé à la question 1.a), la vitesse normale à la paroi est nulle, donc
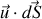 est nul pour les surfaces confondues avec la paroi.
est nul pour les surfaces confondues avec la paroi.
d
Comme nous l'avons vu à la question précédente, les deux équations (1) et (2) ne sont compatibles qu'en supposant que la vitesse possède une composante transverse à proximité de la paroi : c'est l'hypothèse utilisée lors de l'intégration, à la question 1.c), sur la tranche de fluide, et qui implique l'orthogonalité de la vitesse et de la normale à la paroi. Cependant, cette composante n'apparaît pas dans le bilan final, car on effectue un bilan global sur une tranche de fluide.
Si l'on ne tient pas compte de l'existence de cette composante transverse on a alors
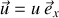 . L'équation de continuité
. L'équation de continuité
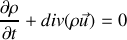
devient :
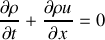
Elle n'est compatible avec la relation (1) que si
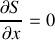
qui est le seul cas où l'hypothèse
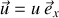 est compatible avec les conditions aux limites.
est compatible avec les conditions aux limites.
Réponse 2
a
La forme générale de l'équation d'Euler pour un fluide inviscide est :
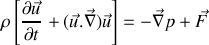
où
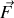 est la résultante des forces volumiques extérieures appliquées au fluide. Dans le problème, on néglige toutes les forces extérieures. De plus, tous les champs considérés ne dépendent que de
est la résultante des forces volumiques extérieures appliquées au fluide. Dans le problème, on néglige toutes les forces extérieures. De plus, tous les champs considérés ne dépendent que de
 et de
et de
 , et on a fait l'hypothèse
, et on a fait l'hypothèse
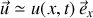 . Ceci conduit à la relation souhaitée :
. Ceci conduit à la relation souhaitée :
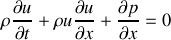
Les deux premiers termes de cette équation représentent la dérivée particulaire
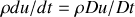 d'un élément de fluide
d'un élément de fluide
 (dérivée en suivant l'élément de fluide). Ils caractérisent l'évolution de l'élément de fluide
(dérivée en suivant l'élément de fluide). Ils caractérisent l'évolution de l'élément de fluide
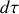 au cours du temps, le terme
au cours du temps, le terme
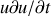 représentant la dérivée convective (ou particulaire) qui traduit le déplacement, par l'ensemble du fluide, de l'élément de fluide au cours du temps.
représentant la dérivée convective (ou particulaire) qui traduit le déplacement, par l'ensemble du fluide, de l'élément de fluide au cours du temps.
Le troisième terme représente quant à lui la résultante des forces de pression s'exerçant sur l'élément de fluide.
b
On s'intéresse désormais aux petits mouvements du fluide autour de l'équilibre. En remplaçant les expressions de
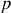 et de
et de
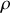 dans l'équation de continuité, on arrive, en se limitant aux termes linéaires en
dans l'équation de continuité, on arrive, en se limitant aux termes linéaires en
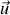 ,
,
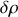 et
et
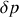 , à :
, à :
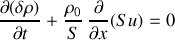
car, à l'équilibre,
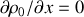 .
.
Pour l'équation d'Euler, un développement analogue conduit à :
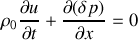
puisqu'à l'équilibre,
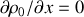 .
.
Si on fait de plus l'hypothèse d'une compression adiabatique du fluide, on peut écrire la relation :
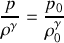
Calculons la différentielle logarithmique de l'expression précédente :
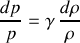
ce qui conduit, pour de petites perturbations autour de l'équilibre, à :
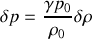
On arrive alors à une nouvelle forme de l'équation d'Euler :
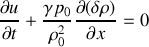
c
En dérivant l'équation de continuité obtenue à la question précédente par rapport au temps, on obtient :
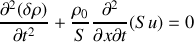
Or,
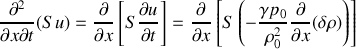
en utilisant la forme de l'équation d'Euler de la question précédente. Posons
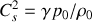 , quantité homogène au carré d'une vitesse ; il vient alors :
, quantité homogène au carré d'une vitesse ; il vient alors :
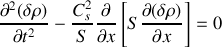
En appliquant la même méthode à l'équation d'Euler, on arrive à :
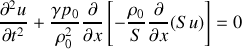
ce qui conduit à l'équation pour la vitesse :
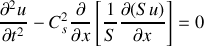
On obtient une équation de propagation pour la petite perturbation autour de l'équilibre ; comme nous allons le voir dans la suite, c'est cette équation qui régit la propagation des ondes sonores dans le fluide.
Réponse 3
a
On considère un pavillon exponentiel, décrit par
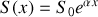 . On peut chercher des solutions de l'équation de la vitesse sous la forme complexe puisque les équations du problème sont linéaires, en posant
. On peut chercher des solutions de l'équation de la vitesse sous la forme complexe puisque les équations du problème sont linéaires, en posant
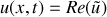 . En remplaçant les expressions de
. En remplaçant les expressions de
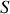 et de
et de
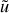 dans l'équation de la vitesse de la question 2.c), nous pouvons écrire :
dans l'équation de la vitesse de la question 2.c), nous pouvons écrire :
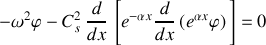
soit
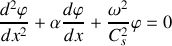
b
Dans le cas d'un tuyau cylindrique,
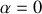 puisque la section est constante. Les solutions de l'équation différentielle sont de la forme :
puisque la section est constante. Les solutions de l'équation différentielle sont de la forme :
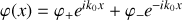
où
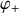 et
et
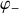 sont deux constantes réelles déterminées par les conditions aux limites. Les solutions du problème se mettent sous la forme
sont deux constantes réelles déterminées par les conditions aux limites. Les solutions du problème se mettent sous la forme
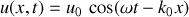
car on ne s'intéresse qu'à des ondes progressives selon
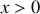 .
.
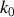 représente le vecteur d'onde des ondes sonores planes progressives se propageant dans le gaz considéré.
représente le vecteur d'onde des ondes sonores planes progressives se propageant dans le gaz considéré.
c
L'équation caractéristique associée à la relation obtenue à la question 3.a) est :
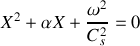
Suivant le signe de son discriminant, trois cas se présentent :
si
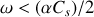 , la solution générale de l'équation différentielle s'écrit sous la forme :
, la solution générale de l'équation différentielle s'écrit sous la forme : 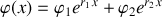
où
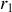 et
et
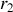 sont les deux racines réelles de l'équation caractéristique. Dans ce cas, il n'y a pas de phénomènes propagatifs dans le pavillon, puisque la solution générale de l'équation de la vitesse est une onde stationnaire. En effet, dans une équation du second degré écrite sous la forme
sont les deux racines réelles de l'équation caractéristique. Dans ce cas, il n'y a pas de phénomènes propagatifs dans le pavillon, puisque la solution générale de l'équation de la vitesse est une onde stationnaire. En effet, dans une équation du second degré écrite sous la forme
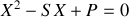 ,
,
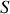 représente la somme des racines et
représente la somme des racines et
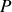 leur produit. Ici, les deux racines
leur produit. Ici, les deux racines
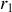 et
et
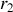 sont de même signe puisque leur produit est positif et ce signe est négatif puisque leur somme est égale à
sont de même signe puisque leur produit est positif et ce signe est négatif puisque leur somme est égale à
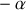 . L'onde est exponentiellement amortie.
. L'onde est exponentiellement amortie.si
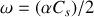 , la solution de l'équation de la vitesse est également une onde stationnaire. Il n'y a donc pas de propagation dans le tuyau.
, la solution de l'équation de la vitesse est également une onde stationnaire. Il n'y a donc pas de propagation dans le tuyau.si
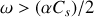 , l'équation caractéristique présente deux racines complexes
, l'équation caractéristique présente deux racines complexes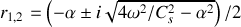
Ceci conduit à des solutions propagatives de forme générale :
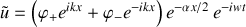
On peut constater que les ondes sonores se propageant dans le pavillon ont une amplitude proportionnelle à
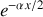 , leur amplitude décroît donc exponentiellement avec
, leur amplitude décroît donc exponentiellement avec
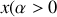 d'après la configuration choisie). Le nouveau nombre d'onde
d'après la configuration choisie). Le nouveau nombre d'onde
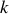 s'exprime sous la forme :
s'exprime sous la forme :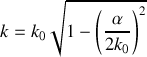
L'expression générale de
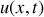 est :
est :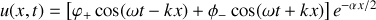
Pour le problème qui nous intéresse, recherchons une solution sous la forme d'une onde progressive se propageant selon les
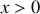 :
: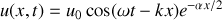
Puisque les ondes ne peuvent se propager que pour
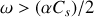 , nous tenons une explication de l'effet “Donald Duck” : les porte-voix qui sont utilisés lors des manifestations peuvent être considérés comme étant constitués de pavillons exponentiels, et le son qui est émis est très nasillard puisqu'il est privé de ses composantes de basse fréquence !
, nous tenons une explication de l'effet “Donald Duck” : les porte-voix qui sont utilisés lors des manifestations peuvent être considérés comme étant constitués de pavillons exponentiels, et le son qui est émis est très nasillard puisqu'il est privé de ses composantes de basse fréquence !
d
La relation de dispersion reliant
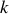 et
et
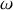 s'obtient à partir de la solution précédente, grâce à l'expression de
s'obtient à partir de la solution précédente, grâce à l'expression de
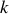 :
:
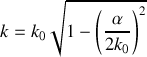
En utilisant la définition de
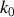 , on obtient l'équation de dispersion sous la forme :
, on obtient l'équation de dispersion sous la forme :
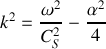
Par définition de la vitesse de phase, on a
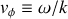 . On en déduit :
. On en déduit :
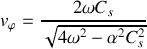
De même, la vitesse de groupe est définie par
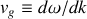 . En différentiant membre à membre la relation de dispersion, il vient
. En différentiant membre à membre la relation de dispersion, il vient
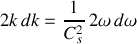
c'est-à-dire :
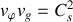
Il s'ensuit que :
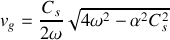
e
D'après la question 3.c), l'expression de l'onde progressive est :
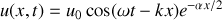
En moyennant sur le temps, on arrive à l'expression de l'énergie cinétique moyenne :
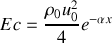
On constate que la quantité
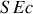 est indépendante de
est indépendante de
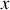 . Ceci n'a rien de surprenant mais traduit la conservation de l'énergie dans le pavillon.
. Ceci n'a rien de surprenant mais traduit la conservation de l'énergie dans le pavillon.




