Comme pour le conducteur isolé, il existe un coefficient positif
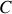 , ne dépendant que de la géométrie et de la position relative des deux conducteurs tel que
, ne dépendant que de la géométrie et de la position relative des deux conducteurs tel que
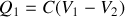
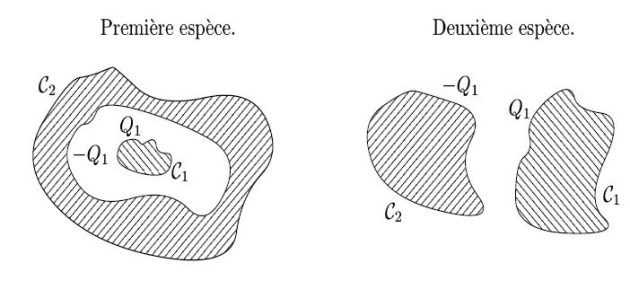
Figure 5 : Exemples de plans de symétrie
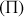 et d'antisymétrie
et d'antisymétrie
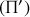 .
.
Exemple :
Le cas le plus simple est celui du condensateur plan. Il est constitué de deux surfaces conductrices chargées parallèles d'aire
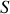 , séparées par une région vide de charge d'épaisseur
, séparées par une région vide de charge d'épaisseur
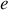 . Pour trouver le potentiel électrostatique régnant dans la région médiane, on applique l'équation de Laplace qui en l'absence de charges se réduit à
. Pour trouver le potentiel électrostatique régnant dans la région médiane, on applique l'équation de Laplace qui en l'absence de charges se réduit à
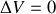 . On suppose que
. On suppose que
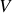 varie uniquement suivant la direction
varie uniquement suivant la direction
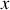 , perpendiculaire aux surfaces (on néglige les effets de bord). Dans ces conditions, l'équation de Laplace s'écrit
, perpendiculaire aux surfaces (on néglige les effets de bord). Dans ces conditions, l'équation de Laplace s'écrit
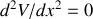 , d'où
, d'où
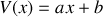 .
.
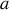 et
et
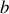 étant deux constantes. En écrivant
étant deux constantes. En écrivant
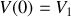 et
et
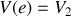 on trouve
on trouve
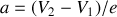 . D'après la définition du potentiel, le champ électrostatique dans le vide intersticiel est alors uniforme de valeur
. D'après la définition du potentiel, le champ électrostatique dans le vide intersticiel est alors uniforme de valeur
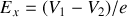 . Le champ étant nul à l'intérieur de la surface conductrice 1, le champ immédiatement à l'extérieur de celle-ci a pour valeur
. Le champ étant nul à l'intérieur de la surface conductrice 1, le champ immédiatement à l'extérieur de celle-ci a pour valeur
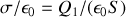 . L'identification des deux expressions conduit à la capacité du condensateur plan :
. L'identification des deux expressions conduit à la capacité du condensateur plan :
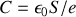 .
.