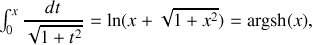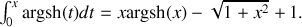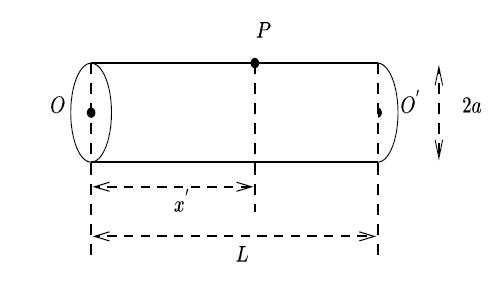
On considère un cylindre de rayon
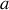et de longueur
(
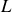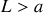, cf. figure 9). Ce cylindre est uniformément chargé en surface, portant la charge totale
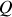. Ce cylindre est placé dans le vide, loin de tout conducteur. Le problème consiste à calculer le potentiel électrique
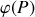en un point
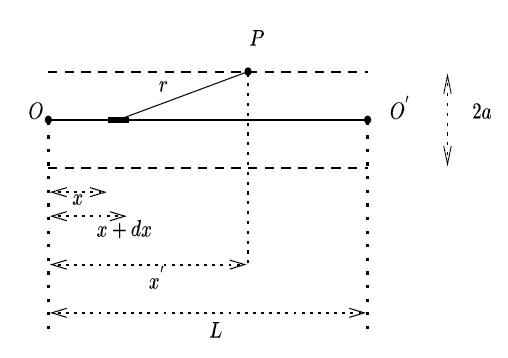
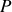à la surface du cylindre. Dans ce calcul, on fera l'approximation suivante : la distribution réelle de charges est remplacée par celle d'un fil rectiligne
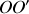(figure 10) de longueur
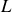, chargé avec la densité linéique
.
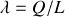Question 1
Ecrire la contribution
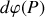au potentiel
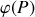d'un élément
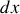du fil.
Question 2
En déduire que l'expression de
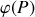est :
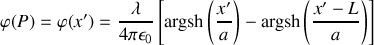
Question 3
Quelle est la forme asymptotique de
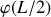lorsque
?
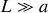Question 4
On considère maintenant un fil infiniment long chargé dont la densité linéique est
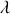. A partir du théorème de GAUSS, calculer le potentiel
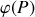créé par ce fil en un point
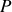situé à une distance
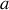du fil. Comparer le résultat obtenu à celui de la question précédente.
Question 5
Si le cylindre de longueur
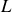finie est métallique, la densité surfacique de charge ne peut plus être constante. Cependant le potentiel
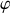l'est. Pourquoi ?
Question 6
On admettra que ce potentiel
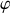constant peut être calculé approximativement en moyennant le potentiel
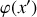obtenu à la question 2. sur toute la longueur
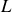du cylindre. Déterminer
.
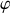Formulaire :
